Flare-On 12 Write-Up
Hi everyone, I'm SuperFashi, a Senior Engineer at GMO Cybersecurity by Ierae, Inc. Just like previous years, I participated in the 11th annual Flare-On reverse engineering challenge. This year I got the 6th place, solving all challenges in around 3 days.
Before going into the write-up, here's a message from our sponsor 😀
Ierae is looking for cybersecurity talents from all over the world! We are a cybersecurity company under GMO Internet Group located in Shibuya, Tokyo, Japan. From forensics and SOC to Web/IoT penetration, we provide a wide range of services and hence need a variety of talents. Our company adapts a flexible work model that includes hybrid work options and flextime. We offer support with relocation to Tokyo, and provide opportunities for remote work from abroad. Japanese language skills are preferred but not required for some departments. If you are interested, please check https://gmo-cybersecurity.com/recruit/contact/ or contact me personally at superfashi@gmo-cybersecurity.com.
1 – Drill Baby Drill!
We are given a game written in Python. Once again, the source code is given because this is the first and easiest challenge, so let's dig into it directly.
The source code is not that long, and we quickly noticed the GenerateFlagText function. We found that there is only one place where it’s called:
if bear_mode:
screen.blit(bearimage, (player.rect.x, screen_height - tile_size))
if current_level == len(LevelNames) - 1 and not victory_mode:
victory_mode = True
flag_text = GenerateFlagText(bear_sum) # <-
print("Your Flag: " + flag_text)
So all we need is to figure out the expected bear_sum value. We also found that there is only one place where the value is updated:
if player.hitBear():
player.drill.retract()
bear_sum *= player.x # <-
bear_mode = True
With the initial bear_sum being 1, we know here that the final bear_sum would be the product of all values of player.x whenever player.hitBear() is True. And looking at the hitBear implementation:
def hitBear(self):
return self.drill.drill_level == max_drill_level
It will be True whenever our drill hits the deepest drill level. However, if you play the game, you will realize you almost always “Hit a Boulder” before you can reach the deepest level. Looking at the code, it corresponds to this logic here:
def hitBoulder(self):
global boulder_layout
boulder_level = boulder_layout[self.x]
return boulder_level == self.drill.drill_level
So what is boulder_layout? We found that it is assigned in the main function:
for i in range(0, tiles_width):
if (i != len(LevelNames[current_level])):
boulder_layout.append(random.randint(2, max_drill_level))
else:
boulder_layout.append(-1)
Essentially, it goes through the entire width of the tiles and places a boulder at a random depth (between 2 and max_drill_level) other than the position where the index is equal to the length of the name of the level.
This means, the correct x to drill down for each level would be exactly the length of the name of the level. Taken together, we have the following solution:
bear_sum = 1
for n in LevelNames:
bear_sum *= len(n)
print(GenerateFlagText(bear_sum))
2 – project_chimera
We are given a single Python file that contains “encrypted data” that the Python code loads and executes.
Whenever we see an exec, we can always just replace it with print to see what exactly the input to exec is; in this case we get:
<code object <module> at 0x7c60f8f1c5a0, file "<genetic_sequencer>", line 1>
A code object is basically a Python bytecode (.pyc), so we can use dis module to disassemble it.
However, be very careful — the Python bytecode differs between minor versions, and can only be correctly read by the same Python minor version. In this case, this Python bytecode is compiled using Python 3.12, so we have to use the same version to disassemble it correctly.
Using dis.dis and dis.show_code on the object, we get:
Name: <module>
Filename: <genetic_sequencer>
Argument count: 0
Positional-only arguments: 0
Kw-only arguments: 0
Number of locals: 0
Stack size: 5
Flags: 0x0
Constants:
0: 0
1: None
2: b'c$|e+O>7&-6`m!Rzak~llE|2<;!(^*VQn#qEH||xE2b$*W=zw8NW~2mgIMj3sFjzy%<NJQ84^$vqeTG&mC+yhlE677j-8)F4nD>~?<GqL64olvBs$bZ4{qE;{|=p@M4Abeb^*>CzIprJ_rCXLX1@k)54$HHULnIe5P-l)Ahj!*6w{D~l%XMwDPu#jDYhX^DN{q5Q|5-Wq%1@lBx}}|vN1p~UI8h)0U&nS13Dg}x8K^E-(q$p0}4!ly-%m{0Hd>^+3*<O{*s0K-lk|}BLHWKJweQrNz5{%F-;@E_{d+ImTl7-o7&}O{%uba)w1RL*UARX*79t+0<^B?zmlODX9|2bzp_ztwjy_TdKb)1%eP4d-Xti0Ygjk_%w!^%1xuMNv4Z8&(*Ue7_^Fby1n3;+G<VDAfqi^h1>0@=Eki5!M~rms%afx`+uxa0*;FzudpqNln5M<@!OqndZ)R<vh4u&gpmmnaMewbT0RJby?(fa7XW#r>ZQ4UE&u|~lZsEY~-lpfWMf0_+pV-H`PXInpwmyo~mZ`tfUK?($KHa%mvNlovZ;Y)D+e6uw+mY6LNB2Y9&akbWpZ@lh=Si<!J@t|CG86E`)jp!l4xEY(h7@$llA4}B9dpL*j)eL{vVcbyMx5_{b13)N@wa~epS8Zfo&V_Y#fM*g9;@6%j=%i%WB0=QS3ewj@0~B!iibu<MqrrJIH{m&FoAGB3#0Nf;x!~dvQ|9#3c})IL6kEvhByJvA{B9%UqX0Tg*-+Ak~NW&RJbB?a6weENW&rzRi2ZB!647HWlA^rG4gvj3Yteo30&*};59;7nJF7eh7vjEXwwxPWWzD*3<IvZS#lIL(l*?u$;EGifKfLDpVb*rXLyw!AP~ZT^-S=4X{31tqe<O1kwG$gBZnu8eva3~6;4CxrcH1{Qg{M;GT5@Bdqt%s{xkT;DyaBk)v>cTr#=XM@cQ-VZZJ1azh{1Df~fwf(mdYk_cEC``#zrevUuf1-I7DHKqx9c7Me?*iNur9a3~o)A1AmHbK!6#k<d+QmXjoUlrAc=R-8EfEvn$TP%?Zb2%`-;wF2Z7c~Qh!QUp%@F7d(Q;It@nl31iwc^NCTTrj*OW)bEH>BYlQ$YmihSV2QDxrCsKNToEmsNif~;-ILG+l$@~sMDcnEHYIbjb?L-swo%>NNY60QJ5`2LX(&$CFf*W(cl7t80939@QH+>;!kK4jMTiOQA}zM@dS+wmk4?RtsqIs(NtuZr(Ewj<zxXaVots!6<}UP5>nNp1gfkes4T*zd{)6h-GF4>NSQO}R*91{c`k!=D-D}baN$1fuVNrUDvGiYVXWYBI456{mCG`ukuZfpN)A<xyb=s}byE(DvZfmpRkvo4CMg+F*3C%f6#?m{g@T4u-G<~mB~wGXg;NVMFDj&f5<)qG1#7xlYdFEQ_jHRu*e&FUmQ1J<Gp}4$xq@yalC(x)S-FIEgQe+IxARLJPRm@DXx&t+<h5L0ORJ<E<cw}6ln6?exLHy}9_dE4pz17oL(~E`{a`E-no7?`5)pDEpNY(-6VaJ?C^<J9(GN!A;n`PTPDZBE;WN>5k=ams`uyy<xmZYd@Og|04{1U(*1PGLR>h3WX?aZWQf~69?j-FsmL^GvInrgidoM2}r1u&}XB+q}oGg-NR#n^X*4uqBy?1qY$4<jzMBhXA);zPfx3*xU!VW$#fFa&MCOfRHVn0%6k8aaRw9dY?)7!uP!nGHEb#k+JxY|2h>kX{N{%!`IfvPX|S@e!nA3Iy~#cKVr)%cFx{mYSGj9h1H_Q6edkhuGk)3Z9gWp`~mJzG74m7(!J^o(!2de`mO?3IDzcV;$RQ`@foiYHlj%{3;+>#iT|K>v-`YH)PTx#fRu(|@AsKT#P^)cna!|9sUyU-MtAxP}M>w|Cc1s4_KI9hlp2y|UAEJ$C2$4Oh6~@uj-!Y-5tEyI$Y%KECN4u6l<*?fcwR_fD^|+djDIJ5u!>A&1N9itm{<3o-un;-)89^#pIPd{VwyzH_1WOyqZ$H)k$XXD-xcUafgjb=N#i!+Onn-Tj-cEob+(!(BOWa>FtC;21DH{%^IHo=c%;r;jstN15qS_U^F=Ab$c5Oh5W?fY!%^vdXfE>5Yf!rHF^<aF`B*be*L=(CF(%-E<?)%b0$BJ)|f2ZjG%ISw+Z8XcC`j+)bpk<79YXWEkdaV7mwG_kiObaNYym&C&ix(EpA7N#?}|aRxAsRm;!2e%e)a4AvZnHUPvwCa?b&OiHoo'
3: '--- Calibrating Genetic Sequencer ---'
4: 'Decoding catalyst DNA strand...'
5: 'Synthesizing Catalyst Serum...'
Names:
0: base64
1: zlib
2: marshal
3: types
4: encoded_catalyst_strand
5: print
6: b85decode
7: compressed_catalyst
8: decompress
9: marshalled_genetic_code
10: loads
11: catalyst_code_object
12: FunctionType
13: globals
14: catalyst_injection_function
0 0 RESUME 0
2 2 LOAD_CONST 0 (0)
4 LOAD_CONST 1 (None)
6 IMPORT_NAME 0 (base64)
8 STORE_NAME 0 (base64)
3 10 LOAD_CONST 0 (0)
12 LOAD_CONST 1 (None)
14 IMPORT_NAME 1 (zlib)
16 STORE_NAME 1 (zlib)
4 18 LOAD_CONST 0 (0)
20 LOAD_CONST 1 (None)
22 IMPORT_NAME 2 (marshal)
24 STORE_NAME 2 (marshal)
5 26 LOAD_CONST 0 (0)
28 LOAD_CONST 1 (None)
30 IMPORT_NAME 3 (types)
32 STORE_NAME 3 (types)
8 34 LOAD_CONST 2 (b'c$|e+O>7&-6`m!Rzak~llE|2<;!(^*VQn#qEH||xE2b$*W=zw8NW~2mgIMj3sFjzy%<NJQ84^$vqeTG&mC+yhlE677j-8)F4nD>~?<GqL64olvBs$bZ4{qE;{|=p@M4Abeb^*>CzIprJ_rCXLX1@k)54$HHULnIe5P-l)Ahj!*6w{D~l%XMwDPu#jDYhX^DN{q5Q|5-Wq%1@lBx}}|vN1p~UI8h)0U&nS13Dg}x8K^E-(q$p0}4!ly-%m{0Hd>^+3*<O{*s0K-lk|}BLHWKJweQrNz5{%F-;@E_{d+ImTl7-o7&}O{%uba)w1RL*UARX*79t+0<^B?zmlODX9|2bzp_ztwjy_TdKb)1%eP4d-Xti0Ygjk_%w!^%1xuMNv4Z8&(*Ue7_^Fby1n3;+G<VDAfqi^h1>0@=Eki5!M~rms%afx`+uxa0*;FzudpqNln5M<@!OqndZ)R<vh4u&gpmmnaMewbT0RJby?(fa7XW#r>ZQ4UE&u|~lZsEY~-lpfWMf0_+pV-H`PXInpwmyo~mZ`tfUK?($KHa%mvNlovZ;Y)D+e6uw+mY6LNB2Y9&akbWpZ@lh=Si<!J@t|CG86E`)jp!l4xEY(h7@$llA4}B9dpL*j)eL{vVcbyMx5_{b13)N@wa~epS8Zfo&V_Y#fM*g9;@6%j=%i%WB0=QS3ewj@0~B!iibu<MqrrJIH{m&FoAGB3#0Nf;x!~dvQ|9#3c})IL6kEvhByJvA{B9%UqX0Tg*-+Ak~NW&RJbB?a6weENW&rzRi2ZB!647HWlA^rG4gvj3Yteo30&*};59;7nJF7eh7vjEXwwxPWWzD*3<IvZS#lIL(l*?u$;EGifKfLDpVb*rXLyw!AP~ZT^-S=4X{31tqe<O1kwG$gBZnu8eva3~6;4CxrcH1{Qg{M;GT5@Bdqt%s{xkT;DyaBk)v>cTr#=XM@cQ-VZZJ1azh{1Df~fwf(mdYk_cEC``#zrevUuf1-I7DHKqx9c7Me?*iNur9a3~o)A1AmHbK!6#k<d+QmXjoUlrAc=R-8EfEvn$TP%?Zb2%`-;wF2Z7c~Qh!QUp%@F7d(Q;It@nl31iwc^NCTTrj*OW)bEH>BYlQ$YmihSV2QDxrCsKNToEmsNif~;-ILG+l$@~sMDcnEHYIbjb?L-swo%>NNY60QJ5`2LX(&$CFf*W(cl7t80939@QH+>;!kK4jMTiOQA}zM@dS+wmk4?RtsqIs(NtuZr(Ewj<zxXaVots!6<}UP5>nNp1gfkes4T*zd{)6h-GF4>NSQO}R*91{c`k!=D-D}baN$1fuVNrUDvGiYVXWYBI456{mCG`ukuZfpN)A<xyb=s}byE(DvZfmpRkvo4CMg+F*3C%f6#?m{g@T4u-G<~mB~wGXg;NVMFDj&f5<)qG1#7xlYdFEQ_jHRu*e&FUmQ1J<Gp}4$xq@yalC(x)S-FIEgQe+IxARLJPRm@DXx&t+<h5L0ORJ<E<cw}6ln6?exLHy}9_dE4pz17oL(~E`{a`E-no7?`5)pDEpNY(-6VaJ?C^<J9(GN!A;n`PTPDZBE;WN>5k=ams`uyy<xmZYd@Og|04{1U(*1PGLR>h3WX?aZWQf~69?j-FsmL^GvInrgidoM2}r1u&}XB+q}oGg-NR#n^X*4uqBy?1qY$4<jzMBhXA);zPfx3*xU!VW$#fFa&MCOfRHVn0%6k8aaRw9dY?)7!uP!nGHEb#k+JxY|2h>kX{N{%!`IfvPX|S@e!nA3Iy~#cKVr)%cFx{mYSGj9h1H_Q6edkhuGk)3Z9gWp`~mJzG74m7(!J^o(!2de`mO?3IDzcV;$RQ`@foiYHlj%{3;+>#iT|K>v-`YH)PTx#fRu(|@AsKT#P^)cna!|9sUyU-MtAxP}M>w|Cc1s4_KI9hlp2y|UAEJ$C2$4Oh6~@uj-!Y-5tEyI$Y%KECN4u6l<*?fcwR_fD^|+djDIJ5u!>A&1N9itm{<3o-un;-)89^#pIPd{VwyzH_1WOyqZ$H)k$XXD-xcUafgjb=N#i!+Onn-Tj-cEob+(!(BOWa>FtC;21DH{%^IHo=c%;r;jstN15qS_U^F=Ab$c5Oh5W?fY!%^vdXfE>5Yf!rHF^<aF`B*be*L=(CF(%-E<?)%b0$BJ)|f2ZjG%ISw+Z8XcC`j+)bpk<79YXWEkdaV7mwG_kiObaNYym&C&ix(EpA7N#?}|aRxAsRm;!2e%e)a4AvZnHUPvwCa?b&OiHoo')
36 STORE_NAME 4 (encoded_catalyst_strand)
10 38 PUSH_NULL
40 LOAD_NAME 5 (print)
42 LOAD_CONST 3 ('--- Calibrating Genetic Sequencer ---')
44 CALL 1
52 POP_TOP
11 54 PUSH_NULL
56 LOAD_NAME 5 (print)
58 LOAD_CONST 4 ('Decoding catalyst DNA strand...')
60 CALL 1
68 POP_TOP
12 70 PUSH_NULL
72 LOAD_NAME 0 (base64)
74 LOAD_ATTR 12 (b85decode)
94 LOAD_NAME 4 (encoded_catalyst_strand)
96 CALL 1
104 STORE_NAME 7 (compressed_catalyst)
13 106 PUSH_NULL
108 LOAD_NAME 1 (zlib)
110 LOAD_ATTR 16 (decompress)
130 LOAD_NAME 7 (compressed_catalyst)
132 CALL 1
140 STORE_NAME 9 (marshalled_genetic_code)
14 142 PUSH_NULL
144 LOAD_NAME 2 (marshal)
146 LOAD_ATTR 20 (loads)
166 LOAD_NAME 9 (marshalled_genetic_code)
168 CALL 1
176 STORE_NAME 11 (catalyst_code_object)
16 178 PUSH_NULL
180 LOAD_NAME 5 (print)
182 LOAD_CONST 5 ('Synthesizing Catalyst Serum...')
184 CALL 1
192 POP_TOP
19 194 PUSH_NULL
196 LOAD_NAME 3 (types)
198 LOAD_ATTR 24 (FunctionType)
218 LOAD_NAME 11 (catalyst_code_object)
220 PUSH_NULL
222 LOAD_NAME 13 (globals)
224 CALL 0
232 CALL 2
240 STORE_NAME 14 (catalyst_injection_function)
22 242 PUSH_NULL
244 LOAD_NAME 14 (catalyst_injection_function)
246 CALL 0
254 POP_TOP
256 RETURN_CONST 1 (None)
In the good ol’ days, we would need to either read the disassembly or use an existing tool like pydecompyle6 or decompyle3 to decompile it (which don’t support 3.12 yet). However, with AI, we can just feed it the above context and have it output human-readable Python code (with extremely good accuracy).

Essentially, it’s the same thing again. So we use the same methodology and get the “decompiled” code of the new marshalled_genetic_code:
import os
import asyncio
import sys
import random
from arc4 import ARC4
import art
import cowsay
import pyjokes
async def activate_catalyst():
# Hardcoded signatures and encrypted data
LEAD_RESEARCHER_SIGNATURE = b'm\x1b@I\x1dAoe@\x07ZF[BL\rN\n\x0cS'
ENCRYPTED_CHIMERA_FORMULA = b'r2b-\r\x9e\xf2\x1fp\x185\x82\xcf\xfc\x90\x14\xf1O\xad#]\xf3\xe2\xc0L\xd0\xc1e\x0c\xea\xec\xae\x11b\xa7\x8c\xaa!\xa1\x9d\xc2\x90'
print('--- Catalyst Serum Injected ---')
print("Verifying Lead Researcher's credentials via biometric scan...")
# Get current user and create signature
current_user = os.getlogin().encode()
# Create user signature using a generator expression with enumerate
user_signature = bytes(c ^ (i + 42) for i, c in enumerate(current_user))
# Small delay for dramatic effect
await asyncio.sleep(0.01)
status = 'pending'
if status == 'pending':
if user_signature == LEAD_RESEARCHER_SIGNATURE:
# Authentication successful
art.tprint('AUTHENTICATION SUCCESS', font='small')
print('Biometric scan MATCH. Identity confirmed as Lead Researcher.')
print('Finalizing Project Chimera...')
# Decrypt the secret formula using ARC4 with current user as key
arc4_decipher = ARC4(current_user)
decrypted_formula = arc4_decipher.decrypt(ENCRYPTED_CHIMERA_FORMULA).decode()
# Reveal the secret!
cowsay.cow('I am alive! The secret formula is:\n' + decrypted_formula)
else:
# Authentication failed
art.tprint('AUTHENTICATION FAILED', font='small')
print('Impostor detected, my genius cannot be replicated!')
print('The resulting specimen has developed an unexpected, and frankly useless, sense of humor.')
# Generate a joke as consolation prize
joke = pyjokes.get_joke(language='en', category='all')
animals = cowsay.char_names[1:] # Skip first character
# Display random animal telling a joke
print(cowsay.get_output_string(random.choice(animals), pyjokes.get_joke()))
sys.exit(1)
else:
print('System error: Unknown experimental state.')
# To run the function:
# asyncio.run(activate_catalyst())
(AI added those comments as well.)
Although the AI-generated code is not 100% correct, at this point the logic is very clear:
ENCRYPTED_CHIMERA_FORMULAis encrypted using ARC4 with the current username as the key.- The current username, bytewise XORed with
(index + 42), has to be equal toLEAD_RESEARCHER_SIGNATURE.
We can then easily solve the challenge:
>>> bytearray(b ^ (i + 42) for i, b in enumerate(b'm\x1b@I\x1dAoe@\x07ZF[BL\rN\n\x0cS'))
bytearray(b'G0ld3n_Tr4nsmut4t10n')
>>> ARC4.new(b'G0ld3n_Tr4nsmut4t10n').decrypt(b'r2b-\r\x9e\xf2\x1fp\x185\x82\xcf\xfc\x90\x14\xf1O\xad#]\xf3\xe2\xc0L\xd0\xc1e\x0c\xea\xec\\
xae\x11b\xa7\x8c\xaa!\xa1\x9d\xc2\x90')
b'Th3_Alch3m1sts_S3cr3t_F0rmul4@flare-on.com'
3 – pretty_devilish_file
This challenge is more on a misc/guessy side. Here’s the thought process I have:
-
First, I tried to decode the PDF directly with the Python library
pdfminer. However, the library throws the exceptionpdfminer.psexceptions.PSEOF: Unexpected EOF. -
By reading the source code/PDF spec, I realized that some of the sections aren’t properly closed. Normally, whenever there’s a
<num> <num> obj, the parser expects to have anendobjcorresponding to it. (Somehow, Chrome can parse a PDF file that doesn’t have it; I’m not sure if it’s spec-defined or not.) -
So I manually added
endobjto the end of4 0 objafterendstream, and for7 0 objas well. -
After the change, the file can be correctly parsed by
pdfminer. -
Looking back at the PDF file, I noticed that object 4 contains this image (and is the only high-entropy content), which probably includes the flag. So I extracted the content using
pdfminer. -
The data after parsing, decryption and decompression is
b"q 612 0 0 10 0 -10 cm\nBI /W 37/H 1/CS/G/BPC 8/L 458/F[\n/AHx\n/DCT\n]ID\nffd8ffe000104a46494600010100000100010000ffdb00430001010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101ffc0000b080001002501011100ffc40017000100030000000000000000000000000006040708ffc400241000000209050100000000000000000000000702050608353776b6b7030436747577ffda0008010100003f00c54d3401dcbbfb9c38db8a7dd265a2159e9d945a086407383aabd52e5034c274e57179ef3bcdfca50f0af80aff00e986c64568c7ffd9\nEI Q \n\nq\nBT\n/ 140 Tf\n10 10 Td\n(Flare-On!)'\nET\nQ\n" -
The hex code
ID\nand before\nEIQis very sus, so I put it into CyberChef and CyberChef immediately recognized that it is an image: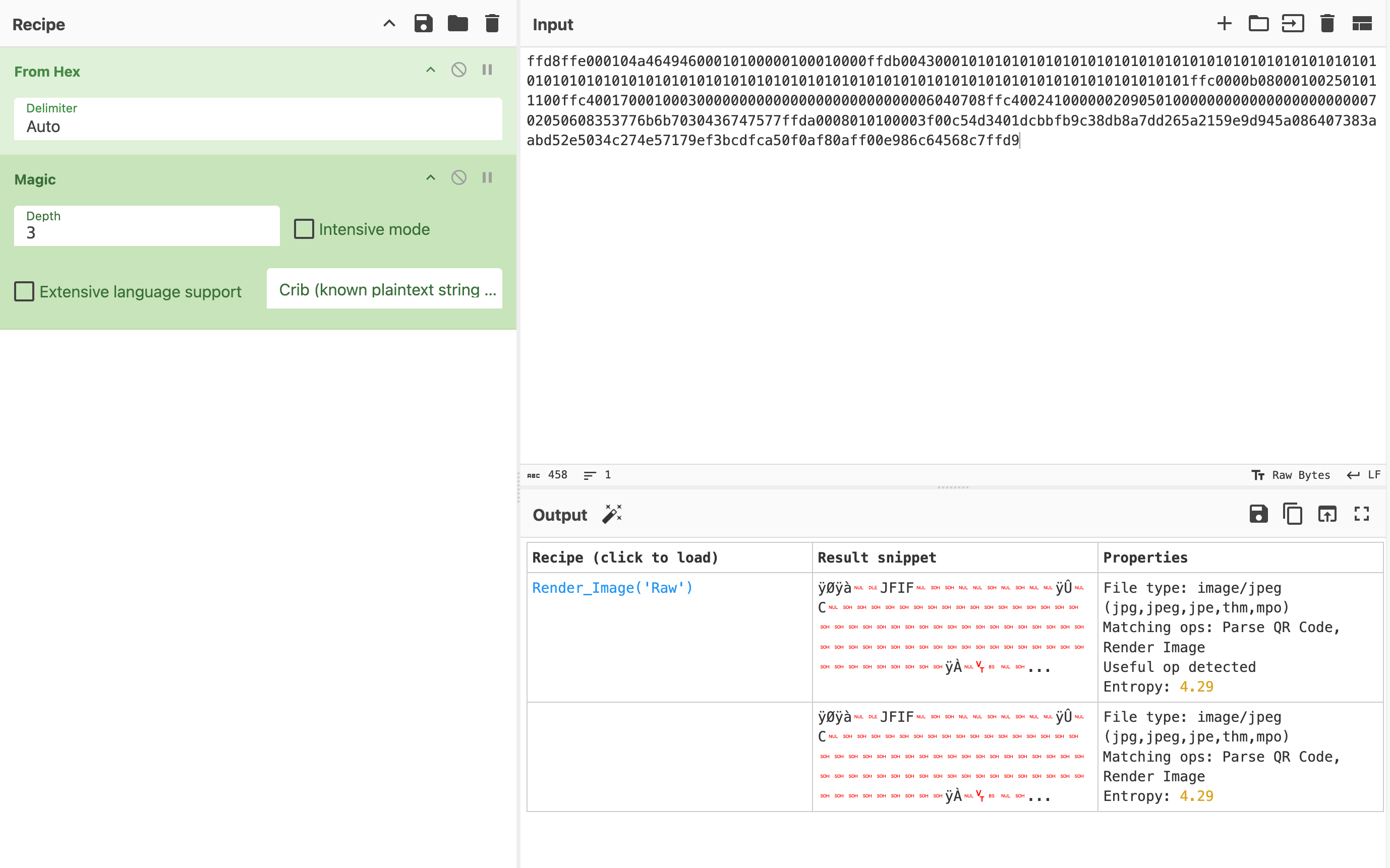
-
Looking at the image, it is only 37 pixels in size. It is very likely that the pixel values represent the flag itself (since they are both in the range of uint8). Using CyberChef, we get the flag:
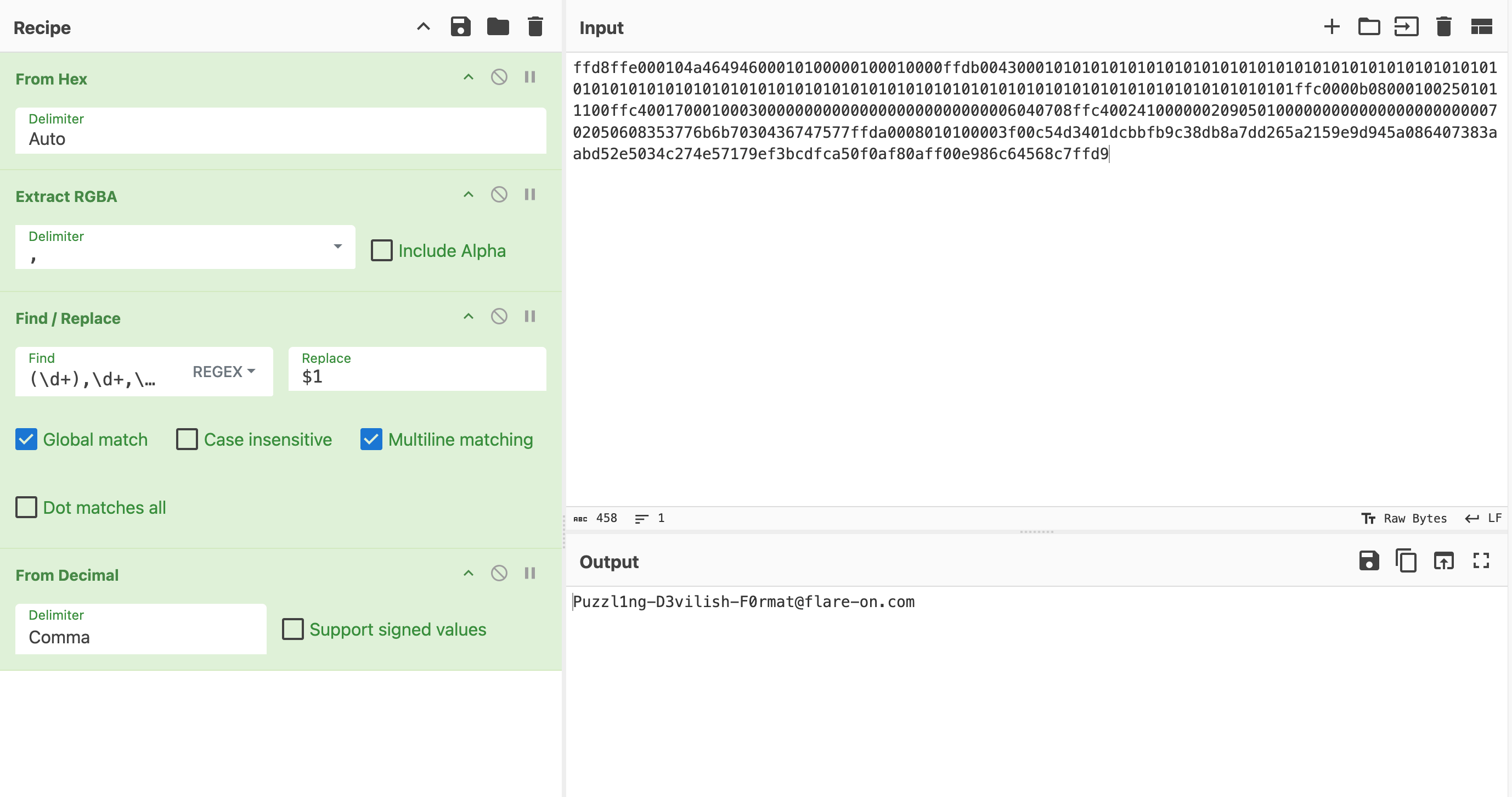
4 – UnholyDragon
The given file has an extension of .exe but it doesn’t actually run out of the box. Opening it with a hex editor, we realized that the initial header magic was somehow corrupted. After fixing the first byte back to a 0x4D, we can run the binary directly. When executed, it starts to generate a new file UnholyDragon-151.exe, which gets run and generates UnholyDragon-152.exe, and so on until UnholyDragon-154.exe, where it stops.
Looking at API captures from our old friend “API Monitor”, we find the following calls that are relevant to the creation of the new binary:
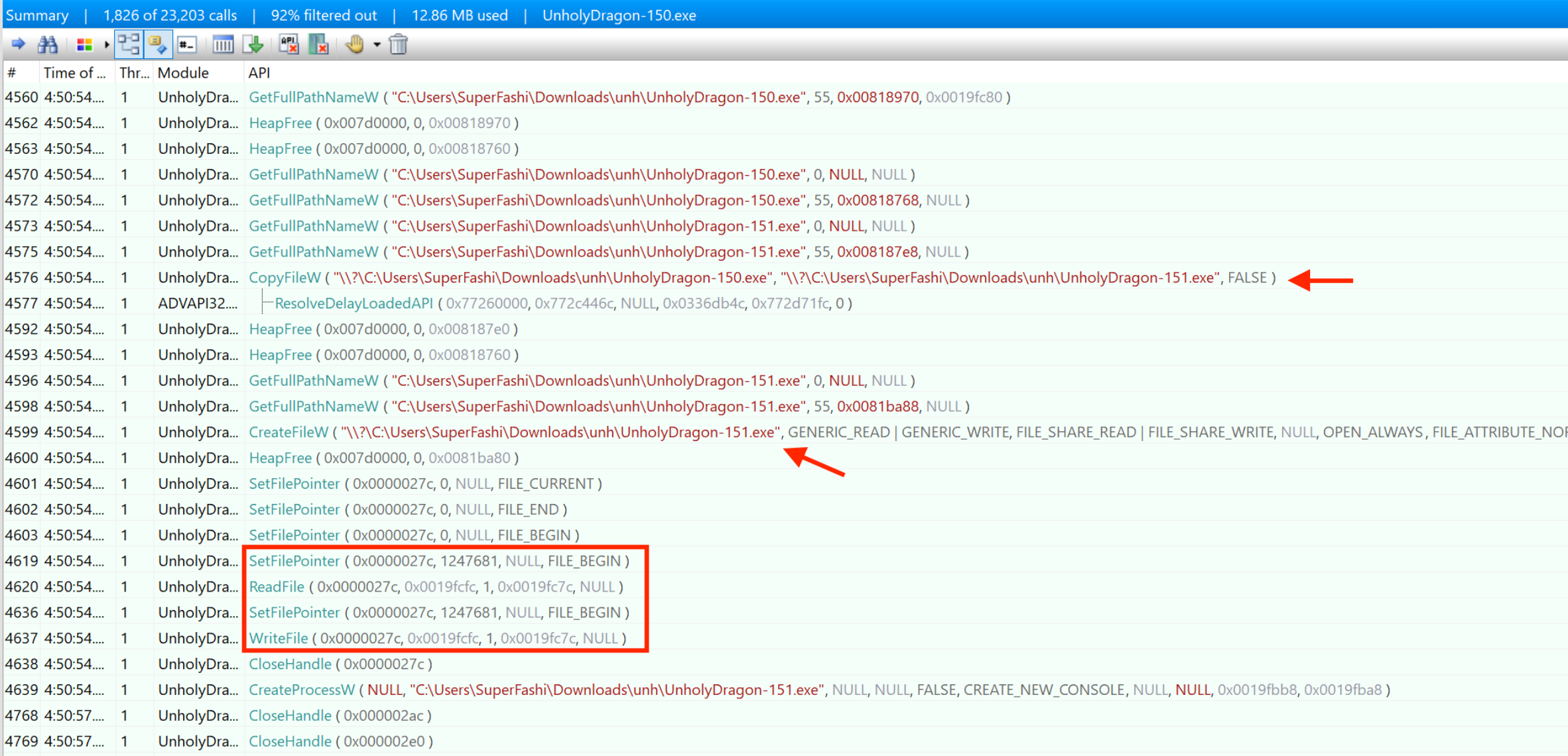
We see that
- A
CopyFileWis called to copy the current binary (150) to a new file (151). - A
CreateFileWis called toopenthe new file. - A sequence of
SetFilePointer(equivalent toseek) andReadFile/WriteFileis called to change only one byte of the file. CreateProcessWis used to execute the new process.
So all we need to figure out is how that byte changed from this binary to the next one. Here, we can use API Monitor’s Call Stack Trace to quickly locate to the calling function. We found that 0x4A8F30 is the “main” function that we are looking for, and the important logic resides here:
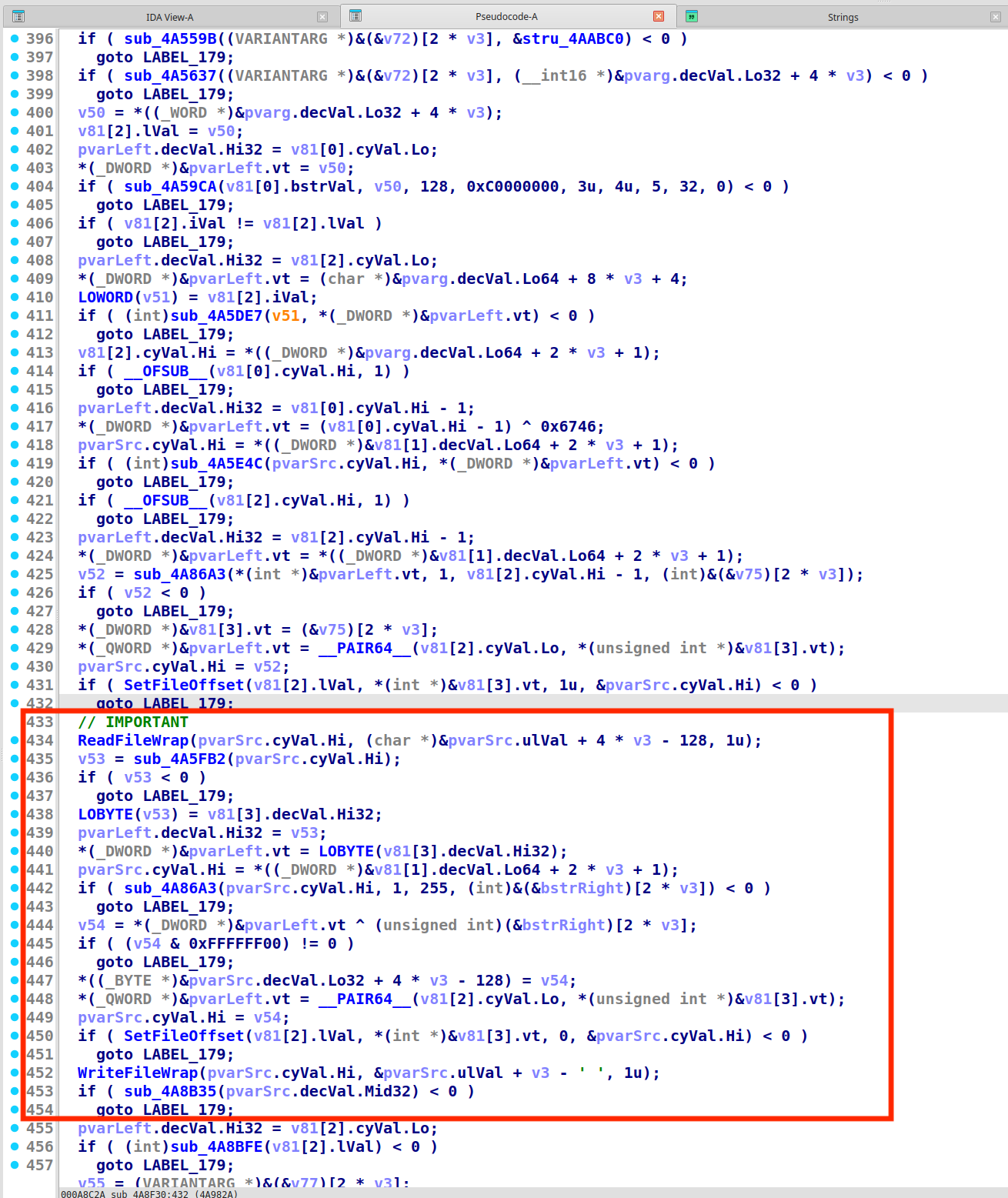
Where one byte is read from the file, and after some calculation, another byte is written back to the same place.
Because this file was compiled from Visual Basic and makes heavy use of the VARIANT type, it was pretty hard to figure out what exactly was done. However, we noticed the following facts:
- The calculation acted on the original byte was only a simple XOR, i.e.
new_byte = old_byte ^ <some calculation>. - The calculation for the XOR byte was based on a fixed buffer that is outside of the range that would be changed by this self-patching process.
So we made an educated guess that, if we were to run the program again, it would restore the original byte by XORing it with the same byte.
You can probably also guess that the initial program was named UnholyDragon-0.exe. After 150 self patches, it arrives at the current state (the given binary).
Therefore, what we did is simply rename the program to UnholyDragon-0.exe and run it. After 150 iterations, we arrive at UnholyDragon-150.exe, where the first byte of the file becomes corrupted. After changing it back to the correct MZ magic, we get the flag directly printed.

5 – ntfsm
For this challenge, the given binary is extremely huge because it contains a very large jump table and many small branches.
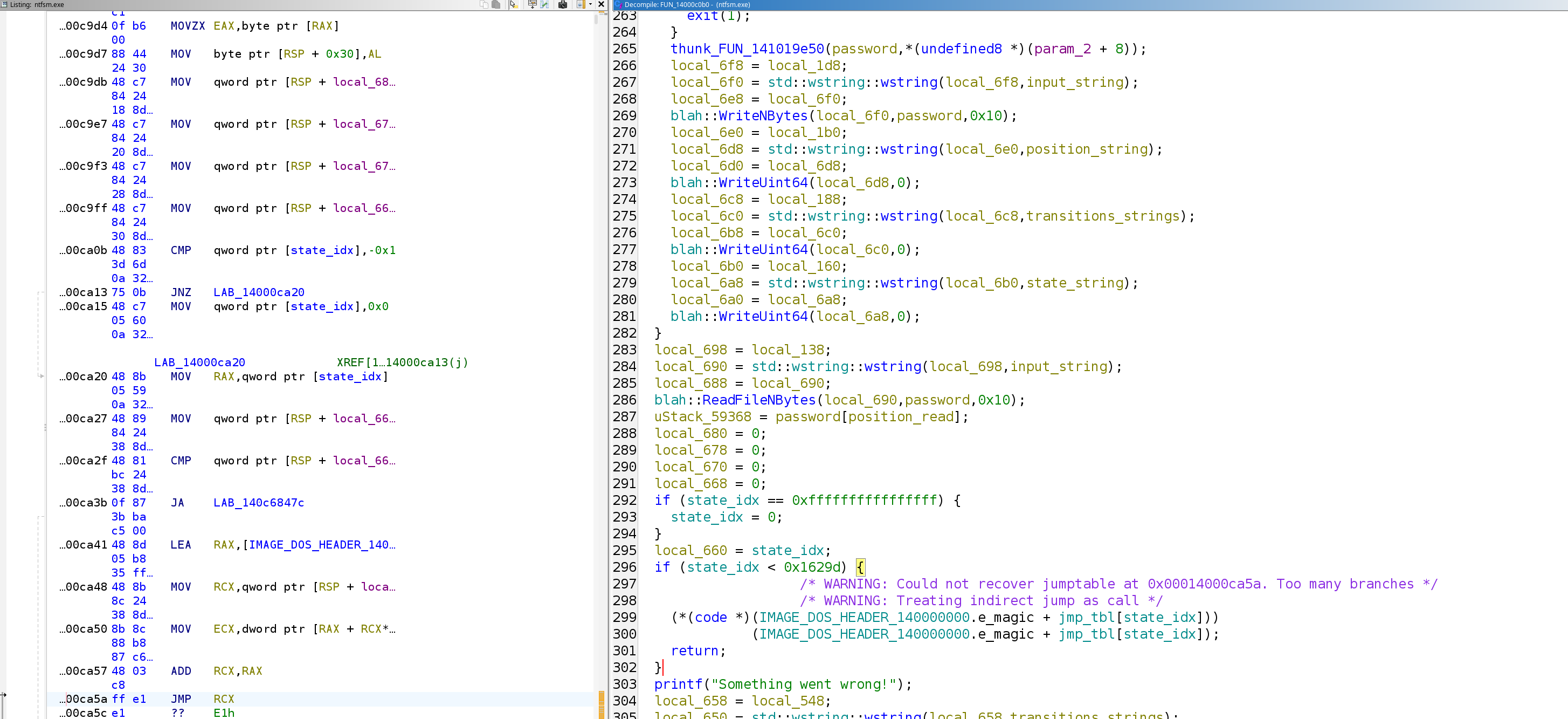
Here, IDA Pro actually did a good job of restoring all the functions. However, for that reason, it becomes very hard to use IDA Pro for this challenge, since IDA will try to recover the entire jump table, making it report “function too big” (even if you increase the size limit. Maybe there’s a way to adjust the jump table limit, but I couldn’t figure that out).
So Ghidra is actually better in this case, where it doesn’t try to expand the entire jump table.
You can approach this challenge either statically or dynamically. Either way, you would see that the file tries to create/access itself but with weird :state or :position appended at the end of the file path. This is actually a feature in NTFS called Alternate Data Streams. I used the Streams tool from Sysinternals, which can read/write ADS for a specific file.
At the beginning, when states are all empty, the program would try to read in 16 characters. It then stores the input into :input, and stores 0 into :position, :transitions, and :state. Then at any given position, it would read that index of the input string, and then jump to the branch indicated by the value of :state inside the jump table:
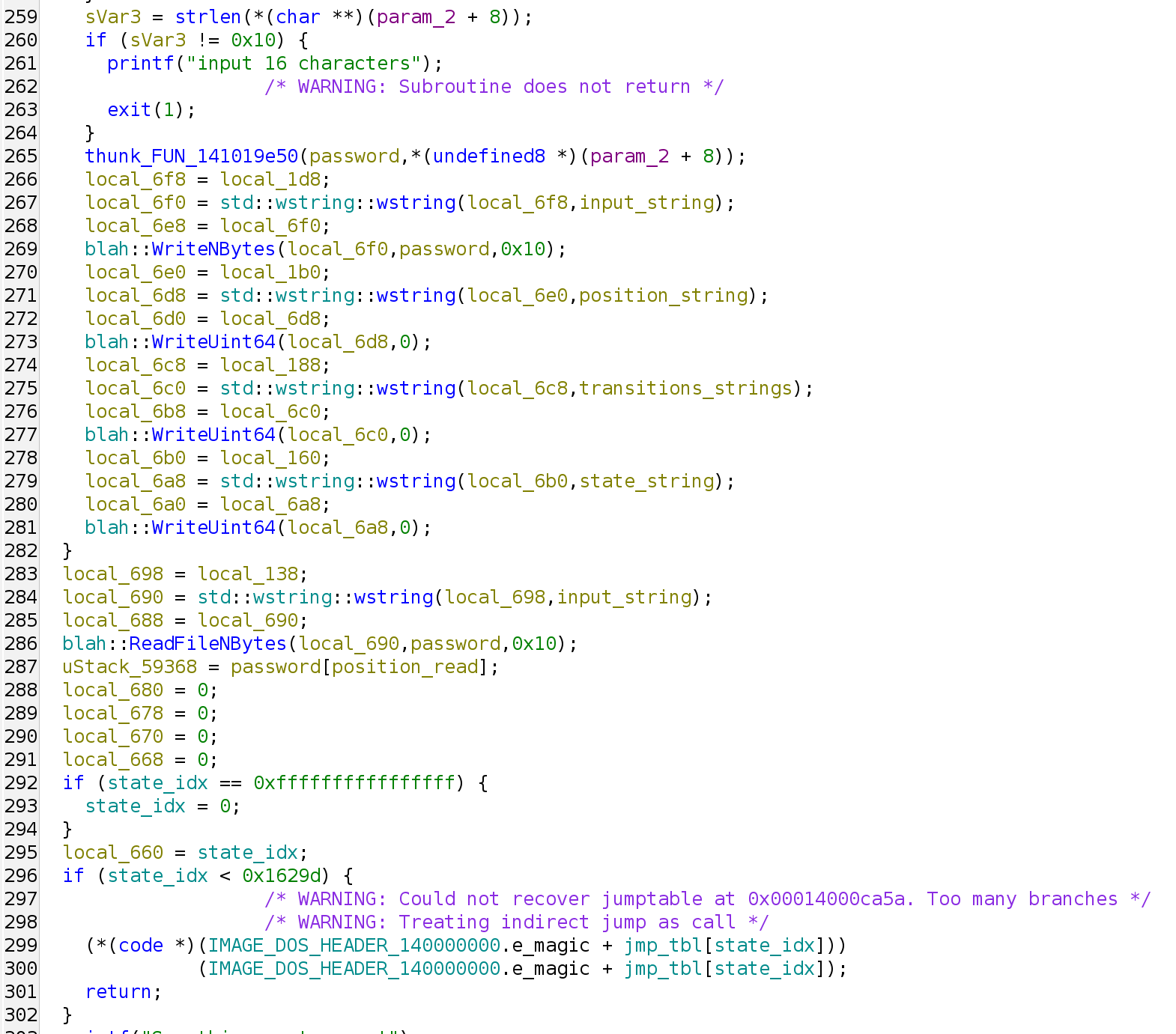
So how do we know what the branch looks like? Here we can do a little patching trick. We first recover one single jump offset (for example, jmp_tbl[0], which in this case is 0x860421).
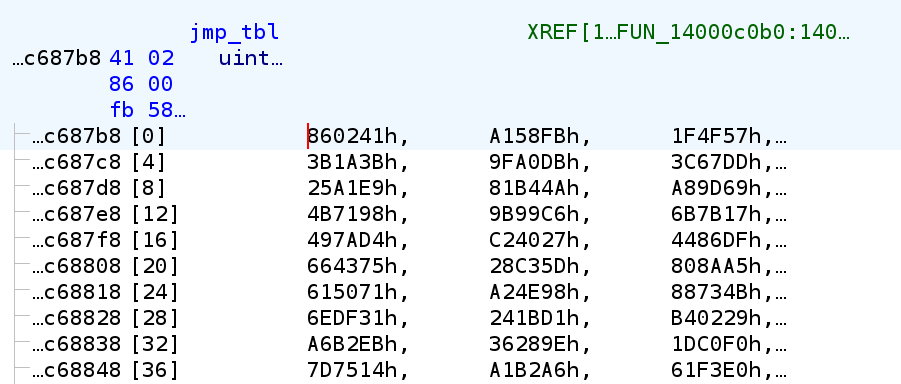
Then we patch the corresponding JMP instruction to directly jump to that location, instead of the indirect jump.
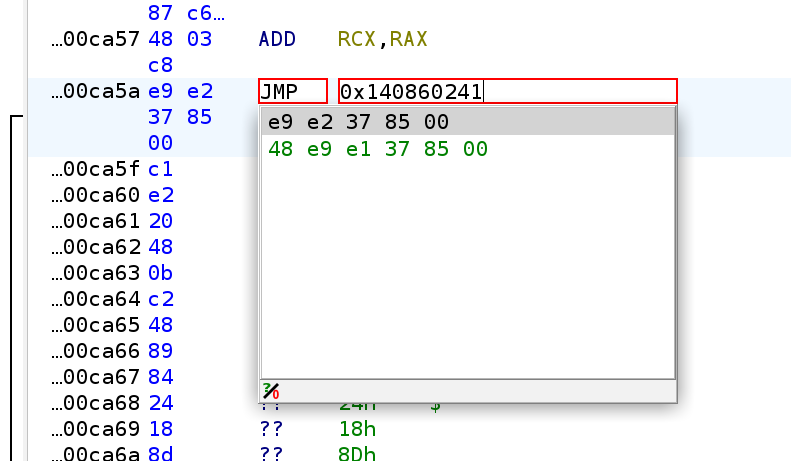
After applying the patch, we look back to our decompiler, and voila, we get our nice decompilation with the context intact:
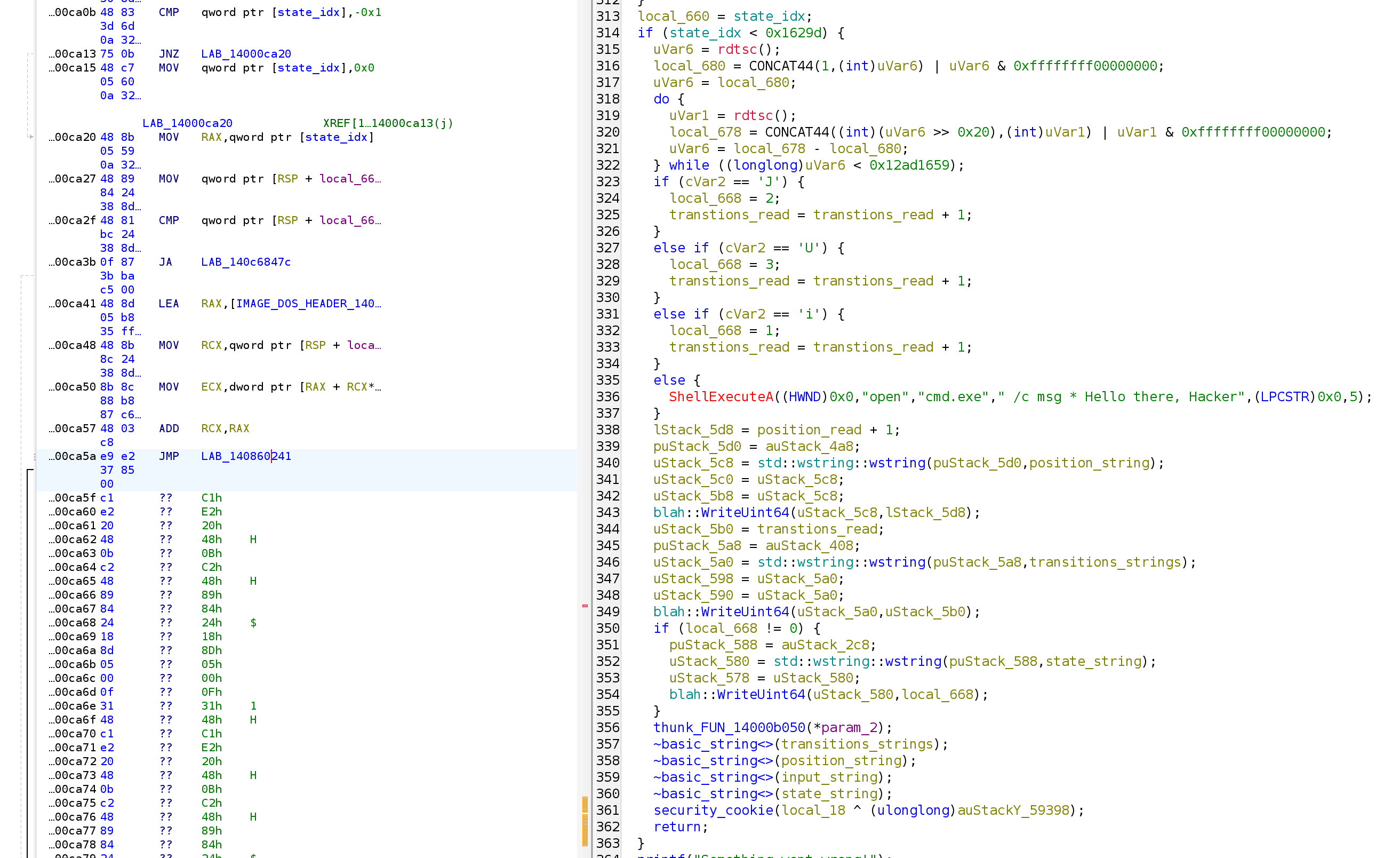
The logic is also easy to read:
- First, there is a
rdtsccall and a loop to intentionally slow down the program, we can just skip that part. - Then there are a few branches for that specific input byte (
cVar2). We see that when the byte isJ, the new state becomes2, when it isU, the new state is3, and when it isi, the new state is1. If none of these, a command is executed that outputs the message “Hello there, Hacker”. - The
:positionvalue is increased by 1, and the:transitionsvalue is increased by 1 if we entered any of the branches that advance the state. These values, along with the:state, are written back to the ADS. - The final
14000b050function would simply start the same program, so that the process is run again with the new states.
And then at the beginning of the decompilation, we see the win condition, which is when both :position and :transitions are 16:

So now we have a basic understanding of how to proceed. We have to find a collection of bytes (the input) that navigates us to the state where both :position and :transitions are 16. This means we have to extract the relation between the branches and the states they lead to. Since the jump table is too large, we can’t possibly do this by hand. That means some kind of parsing is necessary.
Luckily, the parsing is not that hard, as the format is pretty consistent:

Where we see CMPs followed by JZ (when equal), and the final unconditional JMP which leads to an undesirable block. We also see at the beginning of each block there is the assignment for the new :state value. So a simple parser would look something like this (using Capstone):
while True:
insn = insns[idx]
if insn.mnemonic == 'cmp':
assert insn.operands[0].type == capstone.x86.X86_OP_MEM
assert cs_mem_equals(insn.operands[0].mem, st_mem)
assert insn.operands[1].type == capstone.x86.X86_OP_IMM
c = insn.operands[1].imm
assert 0 <= c <= 255
assert c not in branches.values()
assert insns[idx + 1].mnemonic == 'je'
assert insns[idx + 1].operands[0].type == capstone.x86.X86_OP_IMM
addr = insns[idx + 1].operands[0].imm
assert addr not in branches
branches[addr] = c
idx += 2
elif insn.mnemonic == 'jmp':
branches[insn.operands[0].imm] = None
idx += 1
break
else:
raise Exception("Unexpected instruction")
Where branches stores the mapping of the address to the start of the branch, to the character if met at that location.
And then for each of the branch (block), we can have the following parsing function that extracts the new :state value:
while True:
insn = insns[idx]
c = branches[insn.address]
if c is None:
break
assert insn.mnemonic == 'mov'
assert insn.operands[0].type == capstone.x86.X86_OP_MEM
assert insn.operands[0].mem.base == capstone.x86.X86_REG_RSP
assert insn.operands[0].mem.index == 0
assert insn.operands[0].mem.scale == 1
assert insn.operands[0].mem.disp == 0x58d30
assert insn.operands[1].type == capstone.x86.X86_OP_IMM
paths[c] = insn.operands[1].imm
insn = insns[idx + 1]
assert insn.mnemonic == 'mov'
assert insn.operands[0].reg == capstone.x86.X86_REG_RAX
assert insn.operands[1].type == capstone.x86.X86_OP_MEM
assert insn.operands[1].mem.base == capstone.x86.X86_REG_RSP
assert insn.operands[1].mem.index == 0
assert insn.operands[1].mem.scale == 1
assert insn.operands[1].mem.disp == 0x58ab8
insn = insns[idx + 2]
assert insn.mnemonic == 'inc'
assert insn.operands[0].reg == capstone.x86.X86_REG_RAX
insn = insns[idx + 3]
assert insn.mnemonic == 'mov'
assert insn.operands[0].type == capstone.x86.X86_OP_MEM
assert insn.operands[0].mem.base == capstone.x86.X86_REG_RSP
assert insn.operands[0].mem.index == 0
assert insn.operands[0].mem.scale == 1
assert insn.operands[0].mem.disp == 0x58ab8
assert insn.operands[1].reg == capstone.x86.X86_REG_RAX
if idx + 4 >= len(insns):
break
insn = insns[idx + 4]
assert insn.mnemonic == 'jmp'
assert insn.operands[0].type == capstone.x86.X86_OP_IMM
idx += 5
Where paths would store the mapping of the character met at the position to the new :state value that it leads to.
Note that the only important code is
paths[c] = insn.operands[1].imm, everything else was just asserting to make sure the format of that block is what we expect. I personally think this is a good practice, but it definitely slows down my solving speed.
After having the parsing code, we can extract the “graph” that says at any given :state, what character we encounter would lead us to what next :state. Then it is a simple BFS to extract the path:
visited = {0: None}
queue = deque([(0, 0)])
while queue:
u, l = queue.popleft()
if l == 0x10: # win
path = []
while u is not None:
pu = visited[u]
if pu is not None:
path.append(pu[1])
u = pu[0]
else:
break
path.reverse()
print("Path found:", bytes(path))
return
for c, v in graph[u].items():
assert v not in visited
visited[v] = (u, c)
queue.append((v, l + 1))
The solving script with everything together:
from collections import defaultdict, deque
import capstone
data = open('ntfsm.exe', 'rb').read()
IMAGE_BASE = 0x140000000
TEXT_BASE = 0x140001000
TEXT_FILE_BASE = 0x400
TEXT_SIZE = 0x10d06000
def read_text_section(off):
act_off = off - TEXT_BASE + TEXT_FILE_BASE
if act_off < 0:
raise Exception("Invalid read")
return data[act_off:]
def read_uint32(off):
return int.from_bytes(read_text_section(off)[:4], 'little')
Cs = capstone.Cs(capstone.CS_ARCH_X86, capstone.CS_MODE_64)
Cs.detail = True
def cs_mem_equals(m1, m2):
return (m1.segment == m2.segment and
m1.base == m2.base and
m1.index == m2.index and
m1.scale == m2.scale and
m1.disp == m2.disp)
def parse_block(bidx):
TBL = 0x140c687b8
END = 0x140c685ee
off = IMAGE_BASE + read_uint32(TBL + bidx * 4)
if bidx % 100 == 0:
print(f"Parsing block {bidx} at {hex(off)}")
insns = []
for insn in Cs.disasm(read_text_section(off), off, count=101):
if insn.mnemonic == 'jmp' and insn.operands[0].imm == END:
break
insns.append(insn)
if len(insns) > 100:
raise Exception("Too many instructions")
assert insns[0].mnemonic == 'rdtsc'
for index, insn in enumerate(insns[1:], start=1):
if insn.mnemonic == 'movzx' and insn.operands[0].reg == capstone.x86.X86_REG_EAX:
assert insn.operands[1].type == capstone.x86.X86_OP_MEM
mem = insn.operands[1].mem
assert mem.base == capstone.x86.X86_REG_RSP
assert mem.index == 0
assert mem.scale == 1
assert mem.disp == 0x30
idx = index
break
else:
return {}
assert insns[idx + 1].mnemonic == 'mov'
assert insns[idx + 1].operands[0].type == capstone.x86.X86_OP_MEM
assert insns[idx + 1].operands[1].reg == capstone.x86.X86_REG_AL
st_mem = insns[idx + 1].operands[0].mem
rev_sec_tbls = {}
idx += 2
while True:
insn = insns[idx]
if insn.mnemonic == 'cmp':
assert insn.operands[0].type == capstone.x86.X86_OP_MEM
assert cs_mem_equals(insn.operands[0].mem, st_mem)
assert insn.operands[1].type == capstone.x86.X86_OP_IMM
c = insn.operands[1].imm
assert 0 <= c <= 255
assert c not in rev_sec_tbls.values()
assert insns[idx + 1].mnemonic == 'je'
assert insns[idx + 1].operands[0].type == capstone.x86.X86_OP_IMM
addr = insns[idx + 1].operands[0].imm
assert addr not in rev_sec_tbls
rev_sec_tbls[addr] = c
idx += 2
elif insn.mnemonic == 'jmp':
rev_sec_tbls[insn.operands[0].imm] = None
idx += 1
break
else:
raise Exception("Unexpected instruction")
paths = {}
while True:
insn = insns[idx]
c = rev_sec_tbls[insn.address]
if c is None:
break
assert insn.mnemonic == 'mov'
assert insn.operands[0].type == capstone.x86.X86_OP_MEM
assert insn.operands[0].mem.base == capstone.x86.X86_REG_RSP
assert insn.operands[0].mem.index == 0
assert insn.operands[0].mem.scale == 1
assert insn.operands[0].mem.disp == 0x58d30
assert insn.operands[1].type == capstone.x86.X86_OP_IMM
paths[c] = insn.operands[1].imm
insn = insns[idx + 1]
assert insn.mnemonic == 'mov'
assert insn.operands[0].reg == capstone.x86.X86_REG_RAX
assert insn.operands[1].type == capstone.x86.X86_OP_MEM
assert insn.operands[1].mem.base == capstone.x86.X86_REG_RSP
assert insn.operands[1].mem.index == 0
assert insn.operands[1].mem.scale == 1
assert insn.operands[1].mem.disp == 0x58ab8
insn = insns[idx + 2]
assert insn.mnemonic == 'inc'
assert insn.operands[0].reg == capstone.x86.X86_REG_RAX
insn = insns[idx + 3]
assert insn.mnemonic == 'mov'
assert insn.operands[0].type == capstone.x86.X86_OP_MEM
assert insn.operands[0].mem.base == capstone.x86.X86_REG_RSP
assert insn.operands[0].mem.index == 0
assert insn.operands[0].mem.scale == 1
assert insn.operands[0].mem.disp == 0x58ab8
assert insn.operands[1].reg == capstone.x86.X86_REG_RAX
if idx + 4 >= len(insns):
break
insn = insns[idx + 4]
assert insn.mnemonic == 'jmp'
assert insn.operands[0].type == capstone.x86.X86_OP_IMM
idx += 5
return paths
def main():
graph = defaultdict(dict)
for i in range(0x1629d):
paths = parse_block(i)
for c, d in paths.items():
assert c not in graph[i]
graph[i][c] = d
visited = {0: None}
queue = deque([(0, 0)])
while queue:
u, l = queue.popleft()
if l == 0x10:
path = []
while u is not None:
pu = visited[u]
if pu is not None:
path.append(pu[1])
u = pu[0]
else:
break
path.reverse()
print("Path found:", bytes(path))
return
for c, v in graph[u].items():
assert v not in visited
visited[v] = (u, c)
queue.append((v, l + 1))
raise Exception("No path found")
if __name__ == '__main__':
main()
We get the output:
Path found: b'iqg0nSeCHnOMPm2Q'
Input it into the program and it gives the flag back.
6 – Chain of Demands
Reversing
We are given a Linux x86_64 executable. When running it, we see a message chat, and when clicking the Last Convo button we see a record of an existing conversation, with the final two messages redacted. So it is very clear that we have to recover them. And since RSA and LCG appeared, this is actually a crypto-rev challenge.
Take a quick look with your favorite decompiler and you’ll realize that this is another PyInstaller packed binary. Using extremecoders-re/pyinstxtractor, we can extract the entire package into a folder.
The file challenge_to_compile.pyc looked sus from its filename, so let’s start with that. Again, since we are working with compiled Python bytecode, we can use the same technique mentioned in challenge 2, where we disassemble the bytecode using the built-in disassembler, and then feed the whole thing into AI to turn it into something human-readable.
For a .pyc file, something like this would work:
import marshal
import dis
with open('challenge_to_compile.pyc', 'rb') as f:
f.read(16) # Skip header
code = marshal.load(f)
dis.show_code(code)
dis.dis(code)
The decompiled code made by Claude was very complete, so I will not post the entirety here. But it’s worth mentioning that the code generated was so accurate that you could literally run it and it functions exactly the same as the original binary.
The main parts of the logic are in the classes ChatLogic, LCGOracle, and TripleXOROracle:
class LCGOracle:
def __init__(self, multiplier, increment, modulus, initial_seed):
self.multiplier = multiplier
self.increment = increment
self.modulus = modulus
self.state = initial_seed
self.contract_bytes = '6080604052348015600e575f5ffd5b506102e28061001c5f395ff3fe608060405234801561000f575f5ffd5b5060043610610029575f3560e01c8063115218341461002d575b5f5ffd5b6100476004803603810190610042919061010c565b61005d565b6040516100549190610192565b60405180910390f35b5f5f848061006e5761006d6101ab565b5b86868061007e5761007d6101ab565b5b8987090890505f5f8411610092575f610095565b60015b60ff16905081816100a69190610205565b858260016100b49190610246565b6100be9190610205565b6100c89190610279565b9250505095945050505050565b5f5ffd5b5f819050919050565b6100eb816100d9565b81146100f5575f5ffd5b50565b5f81359050610106816100e2565b92915050565b5f5f5f5f5f60a08688031215610125576101246100d5565b5b5f610132888289016100f8565b9550506020610143888289016100f8565b9450506040610154888289016100f8565b9350506060610165888289016100f8565b9250506080610176888289016100f8565b9150509295509295909350565b61018c816100d9565b82525050565b5f6020820190506101a55f830184610183565b92915050565b7f4e487b71000000000000000000000000000000000000000000000000000000005f52601260045260245ffd5b7f4e487b71000000000000000000000000000000000000000000000000000000005f52601160045260245ffd5b5f61020f826100d9565b915061021a836100d9565b9250828202610228816100d9565b9150828204841483151761023f5761023e6101d8565b5b5092915050565b5f610250826100d9565b915061025b836100d9565b9250828203905081811115610273576102726101d8565b5b92915050565b5f610283826100d9565b915061028e836100d9565b92508282019050808211156102a6576102a56101d8565b5b9291505056fea2646970667358221220c7e885c1633ad951a2d8168f80d36858af279d8b5fe2e19cf79eac15ecb9fdd364736f6c634300081e0033'
self.contract_abi = [{'inputs': [{'internalType': 'uint256', 'name': 'LCG_MULTIPLIER', 'type': 'uint256'}, {'internalType': 'uint256', 'name': 'LCG_INCREMENT', 'type': 'uint256'}, {'internalType': 'uint256', 'name': 'LCG_MODULUS', 'type': 'uint256'}, {'internalType': 'uint256', 'name': '_currentState', 'type': 'uint256'}, {'internalType': 'uint256', 'name': '_counter', 'type': 'uint256'}], 'name': 'nextVal', 'outputs': [{'internalType': 'uint256', 'name': '', 'type': 'uint256'}], 'stateMutability': 'pure', 'type': 'function'}]
self.deployed_contract = None
def deploy_lcg_contract(self):
self.deployed_contract = SmartContracts.deploy_contract(self.contract_bytes, self.contract_abi)
def get_next(self, counter):
print(f'\n[+] Calling nextVal() with _currentState={self.state}')
self.state = self.deployed_contract.functions.nextVal(
self.multiplier, self.increment, self.modulus,
self.state, counter
).call()
print(f' _counter = {counter}: Result = {self.state}')
return self.state
class TripleXOROracle:
def __init__(self):
self.contract_bytes = '61030f61004d600b8282823980515f1a6073146041577f4e487b71000000000000000000000000000000000000000000000000000000005f525f60045260245ffd5b305f52607381538281f3fe7300000000000000000000000000000000000000003014608060405260043610610034575f3560e01c80636230075614610038575b5f5ffd5b610052600480360381019061004d919061023c565b610068565b60405161005f91906102c0565b60405180910390f35b5f5f845f1b90505f845f1b90505f61007f85610092565b9050818382181893505050509392505050565b5f5f8290506020815111156100ae5780515f525f5191506100b6565b602081015191505b50919050565b5f604051905090565b5f5ffd5b5f5ffd5b5f819050919050565b6100df816100cd565b81146100e9575f5ffd5b50565b5f813590506100fa816100d6565b92915050565b5f5ffd5b5f5ffd5b5f601f19601f8301169050919050565b7f4e487b71000000000000000000000000000000000000000000000000000000005f52604160045260245ffd5b61014e82610108565b810181811067ffffffffffffffff8211171561016d5761016c610118565b5b80604052505050565b5f61017f6100bc565b905061018b8282610145565b919050565b5f67ffffffffffffffff8211156101aa576101a9610118565b5b6101b382610108565b9050602081019050919050565b828183375f83830152505050565b5f6101e06101db84610190565b610176565b9050828152602081018484840111156101fc576101fb610104565b5b6102078482856101c0565b509392505050565b5f82601f83011261022357610222610100565b5b81356102338482602086016101ce565b91505092915050565b5f5f5f60608486031215610253576102526100c5565b5b5f610260868287016100ec565b9350506020610271868287016100ec565b925050604084013567ffffffffffffffff811115610292576102916100c9565b5b61029e8682870161020f565b9150509250925092565b5f819050919050565b6102ba816102a8565b82525050565b5f6020820190506102d35f8301846102b1565b9291505056fea26469706673582212203fc7e6cc4bf6a86689f458c2d70c565e7c776de95b401008e58ca499ace9ecb864736f6c634300081e0033'
self.contract_abi = [{'inputs': [{'internalType': 'uint256', 'name': '_primeFromLcg', 'type': 'uint256'}, {'internalType': 'uint256', 'name': '_conversationTime', 'type': 'uint256'}, {'internalType': 'string', 'name': '_plaintext', 'type': 'string'}], 'name': 'encrypt', 'outputs': [{'internalType': 'bytes32', 'name': '', 'type': 'bytes32'}], 'stateMutability': 'pure', 'type': 'function'}]
self.deployed_contract = None
def deploy_triple_xor_contract(self):
self.deployed_contract = SmartContracts.deploy_contract(self.contract_bytes, self.contract_abi)
def encrypt(self, prime_from_lcg, conversation_time, plaintext_bytes):
print(f'\n[+] Calling encrypt() with prime_from_lcg={prime_from_lcg}, time={conversation_time}, plaintext={plaintext_bytes}')
ciphertext = self.deployed_contract.functions.encrypt(
prime_from_lcg, conversation_time, plaintext_bytes
).call()
print(f' _ciphertext = {ciphertext.hex()}')
return ciphertext
class ChatLogic:
def __init__(self):
self.lcg_oracle = None
self.xor_oracle = None
self.rsa_key = None
self.seed_hash = None
self.super_safe_mode = False
self.message_count = 0
self.conversation_start_time = 0
self.chat_history = []
self._initialize_crypto_backend()
def _get_system_artifact_hash(self):
artifact = platform.node().encode('utf-8')
hash_val = hashlib.sha256(artifact).digest()
seed_hash = int.from_bytes(hash_val, 'little')
print(f'[SETUP] - Generated Seed {seed_hash}...')
return seed_hash
def _generate_primes_from_hash(self, seed_hash):
primes = []
current_hash_byte_length = (seed_hash.bit_length() + 7) // 8
current_hash = seed_hash.to_bytes(current_hash_byte_length, 'little')
print('[SETUP] Generating LCG parameters from system artifact...')
iteration_limit = 10000
iterations = 0
while len(primes) < 3 and iterations < iteration_limit:
current_hash = hashlib.sha256(current_hash).digest()
candidate = int.from_bytes(current_hash, 'little')
iterations += 1
if candidate.bit_length() == 256 and isPrime(candidate):
primes.append(candidate)
print(f'[SETUP] - Found parameter {len(primes)}: {str(candidate)[:20]}...')
if len(primes) < 3:
error_msg = '[!] Error: Could not find 3 primes within iteration limit.'
print(f'Current Primes: ', primes)
print(error_msg)
exit()
return primes[0], primes[1], primes[2]
def _initialize_crypto_backend(self):
self.seed_hash = self._get_system_artifact_hash()
m, c, n = self._generate_primes_from_hash(self.seed_hash)
self.lcg_oracle = LCGOracle(m, c, n, self.seed_hash)
self.lcg_oracle.deploy_lcg_contract()
print('[SETUP] LCG Oracle is on-chain...')
self.xor_oracle = TripleXOROracle()
self.xor_oracle.deploy_triple_xor_contract()
print('[SETUP] Triple XOR Oracle is on-chain...')
print('[SETUP] Crypto backend initialized...')
def generate_rsa_key_from_lcg(self):
print('[RSA] Generating RSA key from on-chain LCG primes...')
lcg_for_rsa = LCGOracle(
self.lcg_oracle.multiplier,
self.lcg_oracle.increment,
self.lcg_oracle.modulus,
self.seed_hash
)
lcg_for_rsa.deploy_lcg_contract()
primes_arr = []
rsa_msg_count = 0
iteration_limit = 10000
iterations = 0
while len(primes_arr) < 8 and iterations < iteration_limit:
candidate = lcg_for_rsa.get_next(rsa_msg_count)
rsa_msg_count += 1
iterations += 1
if candidate.bit_length() == 256 and isPrime(candidate):
primes_arr.append(candidate)
print(f'[RSA] - Found 256-bit prime #{len(primes_arr)}')
print('Primes Array: ', primes_arr)
if len(primes_arr) < 8:
error_msg = '[RSA] Error: Could not find 8 primes within iteration limit.'
print('Current Primes: ', primes_arr)
print(error_msg)
return error_msg
n = 1
for p_val in primes_arr:
n *= p_val
phi = 1
for p_val in primes_arr:
phi *= (p_val - 1)
e = 65537
if math.gcd(e, phi) != 1:
error_msg = '[RSA] Error: Public exponent e is not coprime with phi(n). Cannot generate key.'
print(error_msg)
return error_msg
self.rsa_key = RSA.construct((n, e))
try:
with open('public.pem', 'wb') as f:
f.write(self.rsa_key.export_key('PEM'))
print("[RSA] Public key generated and saved to 'public.pem'")
return 'Public key generated and saved successfully.'
except Exception as e:
print(f'[RSA] Error saving key: {e}')
return f'Error saving key: {e}'
def process_message(self, plaintext):
if self.conversation_start_time == 0:
self.conversation_start_time = time.time()
conversation_time = int(time.time() - self.conversation_start_time)
if self.super_safe_mode and self.rsa_key:
plaintext_bytes = plaintext.encode('utf-8')
plaintext_enc = bytes_to_long(plaintext_bytes)
_enc = pow(plaintext_enc, self.rsa_key.e, self.rsa_key.n)
ciphertext = _enc.to_bytes(self.rsa_key.n.bit_length(), 'little').rstrip(b'\x00')
encryption_mode = 'RSA'
plaintext = '[ENCRYPTED]'
else:
prime_from_lcg = self.lcg_oracle.get_next(self.message_count)
ciphertext = self.xor_oracle.encrypt(prime_from_lcg, conversation_time, plaintext)
encryption_mode = 'LCG-XOR'
log_entry = {
'conversation_time': conversation_time,
'mode': encryption_mode,
'plaintext': plaintext,
'ciphertext': ciphertext.hex()
}
self.chat_history.append(log_entry)
self.message_count += 1
self.save_chat_log()
return f'[{conversation_time}s] {plaintext}', f'[{conversation_time}s] {ciphertext.hex()}'
def save_chat_log(self):
try:
with open('chat_log.json', 'w') as f:
json.dump(self.chat_history, f, indent=2)
except Exception as e:
print(f'Error saving chat log: {e}')
Essentially:
- The program begins by generating a
seed_hash, which is then used to generate 3 primesm,c, andn. - The 3 primes together with
seed_hashare used inLCGOracle. - The 3 primes and
seed_hashare also used for generating the RSA key pair. LCGOracleandTripleXOROracle’s implementations are actually Solidity contracts deployed on-chain.
Let’s use Dedaub to decompile the contracts. First for LCGOracle:
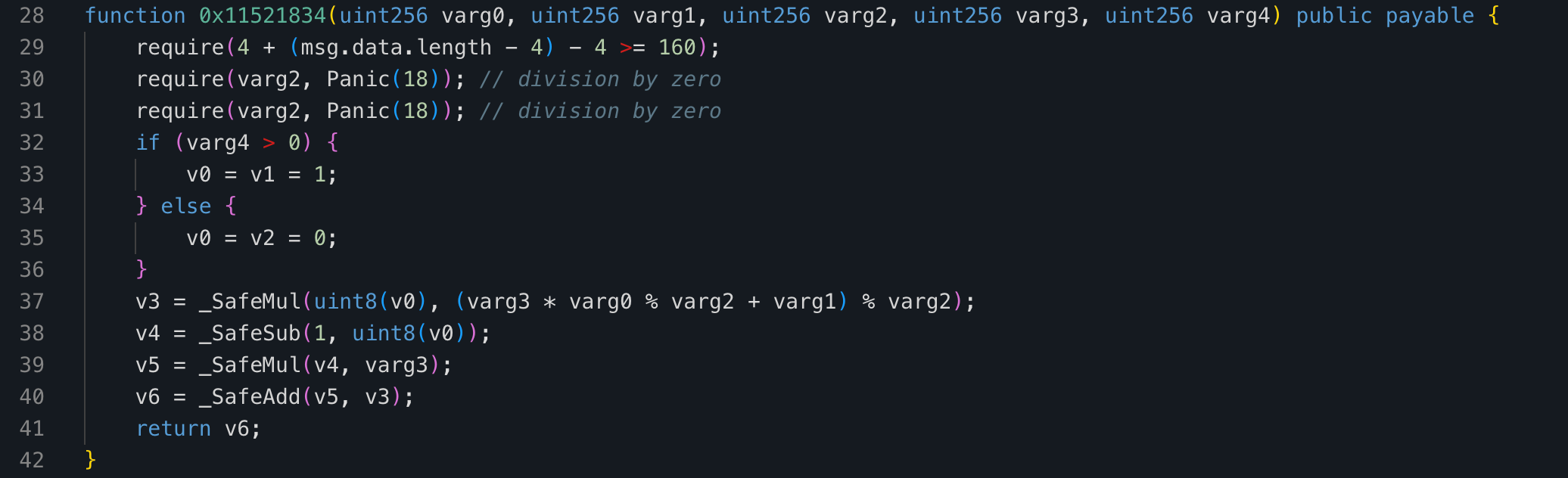
We see that it is equivalent to the following:
if varg4 == 0:
return varg3
return (varg3 * varg0 + varg1) % varg2
Given that we already know the input from the contract ABI and variable name, we can rewrite LCGOracle::gen_next as
def gen_next(self, counter):
if counter == 0:
return self.state
self.state = (self.multiplier * self.state + self.increment) % self.modulus
return self.state
Then for TripleXOROracle, we have the decompilation:

Which is essentially just the inputs XORed together.
Then, the bug becomes very obvious:
- Notice that
counterforgen_nextis essentially the message index. Therefore, for the first message,LCGOraclewould directly returnself.state. - If we look at
self.state, we find that it is initialized to be exactlyseed_hash. - We also know the
conversation_timeof the first message (since it is recorded in the conversation log), and it is always 0-based according to the logic. - This means the first message sent is simply
cipher = plain ^ seed_hash ^ 0.
Since we know the ciphertext and plaintext, we can trivially derive the seed_hash. Easy!
However, after putting the seed_hash we got into generate_primes_from_hash and consequently generate_rsa_key_from_lcg, we don’t get the same RSA key as was used to encrypt the conversation.
I spent so much time on this, checking if I missed anything, only to realize that this challenge was actually unsolvable. The conversation recorded does not actually follow the logic of the code.
This just reminds me of another challenge that involves Web3 and ends up being unsolvable.
Crypto
Is there another way to recover what we need? Turns out there is, but since I’m not a crypto player, AI comes to the rescue:

Essentially, for any three points \((x_1, y_1)\), \((x_2, y_2)\), \((x_3, y_3)\), they satisfy:
y_i \equiv ax_i + b \mod c
$$
By eliminating \(a\) and \(b\), we get the constraint:
(y_1 – y_2)(x_2 – x_3) – (y_2 – y_3)(x_1 – x_2) \equiv 0 \mod c
$$
This means \(c\) divides the expression:
D = (y₁ – y₂)(x₂ – x₃) – (y₂ – y₃)(x₁ – x₂)
$$
With all messages we know, we can compute the expression \(D_{i,j,k}\) for all possible triplets. Compute \(c=\gcd(D_{i,j,k})\) of all these expressions. After we get \(c\), we can just solve for \(a\) and \(b\) using any two points:
\begin{align*}
a &\equiv \frac{y_1 – y_2}{x_1 – x_2} &\mod c\\
b &\equiv y_1 – a\cdot x_1 &\mod c
\end{align*}
$$
In Python, this would look like:
Ds = []
for i in range(len(points)):
for j in range(i+1, len(points)):
for k in range(j+1, len(points)):
_1 = points[i]
_2 = points[j]
_3 = points[k]
D = (_1[1] - _2[1]) * (_2[0] - _3[0]) - (_2[1] - _3[1]) * (_1[0] - _2[0])
Ds.append(D)
modulus = math.gcd(Ds[0], Ds[1])
for d in Ds[2:]:
modulus = math.gcd(modulus, d)
assert isPrime(modulus)
print(f'Modulus: {modulus}')
_1 = points[0]
_2 = points[1]
A = (_1[1] - _2[1]) * pow(_1[0] - _2[0], -1, modulus) % modulus
B = (_1[1] - A * _1[0]) % modulus
print(f'A: {A}\nB: {B}')
Which gives us output
Modulus: 98931271253110664660254761255117471820360598758511684442313187065390755933409
A: 11352347617227399966276728996677942514782456048827240690093985172111341259890
B: 61077733451871028544335625522563534065222147972493076369037987394712960199707
Note that A is not a prime number; this means that this set of parameters is definitely not generated from the code that was distributed.
Anyway, now we have these, we have all four parameters needed to generate the RSA key. After generation, we confirmed that the modulus is equivalent to the one used in the conversation. Using textbook RSA, we can recover the messages successfully.
7 – The Boss Needs Help
Opening the binary up, we get bombarded by this huge array of expressions.

These expressions are what’s called Mixed Boolean Arithmetic and are what all the cool kids like to use for obfuscating their binaries nowadays.
Deobfuscation
Luckily, I have some prior research on MBA, as can be seen here. One of my biggest observations is that an MBA expression usually involves a number to operate against. This number cannot be a constant, as constant propagation would easily eliminate it. This means the number is often chosen from unallocated stack or the data section, so constant propagation cannot work because it cannot make assumptions about whether the memory is volatile.
However, this also means the obfuscator cannot make any assumption on the value as well, so it must support any value to be involved in the obfuscation, and the MBA expressions must act on the entire range of possible values.
Now, taking a closer look at the main function above, we realized that the MBA expressions are trying to read from 0x14047a3b0, which is in the data section. Since we know that the obfuscation should work regardless of the actual value, let’s try patching the first memory read to a 0 immediate value:

Which gives us the following decompiled code:
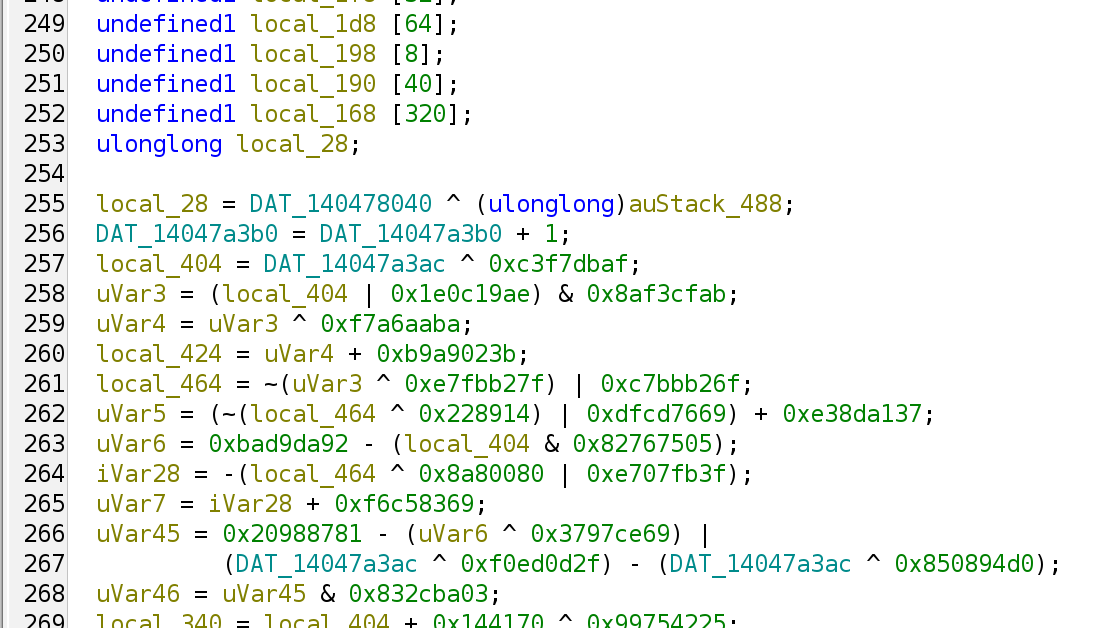
As you can see, the entire MBA is constant-propagated and folded into a single expression of + 1.
I was actually using both Ghidra and IDA Pro for decompiling, and sometimes Ghidra performs better on constant propagation, but other times IDA Pro can eliminate more instructions.
To validate that the value doesn’t matter, we can patch it to another value like 0xdeadbeef:
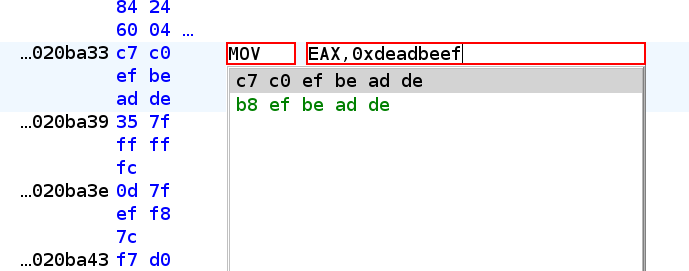
And we see that the code is exactly the same:
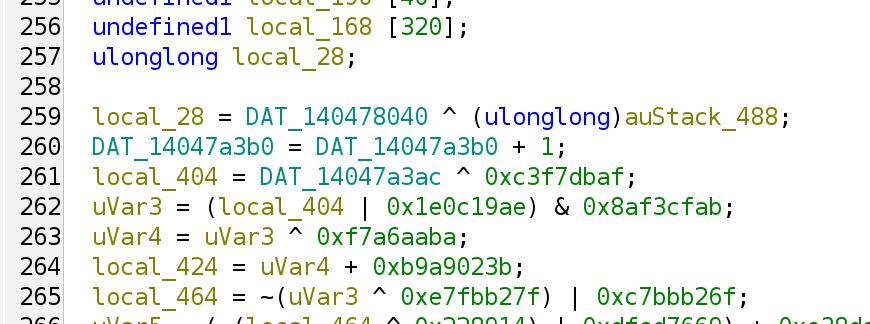
We can do the same patching to that read of DAT_14047a3ac, where the code would turn to
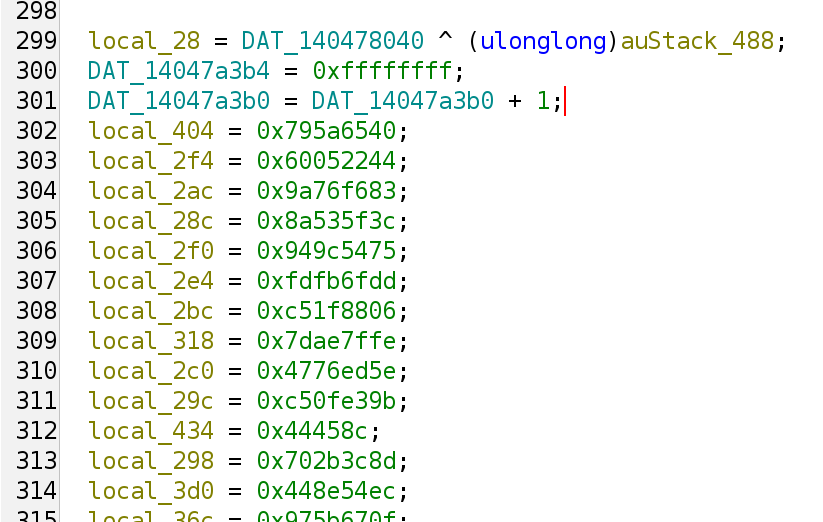
Note that we have a lot of stack variable assignments that unfortunately doesn’t eliminate, but that’s fine as we can simply skip past these stack assignments.

Notice that the nasty MBAs have finally gone and the function calls are exposed to us directly.
Patching read by hand is definitely painful. After some observation, we realized that the MBA expressions is actually reading from the following addresses only: 0x14047a3ac, 0x14047a3b0, and 0x14047a3b4. So all we need to do is to find cross references to these addresses, and patch those MOV reads to MOV from immediate value (where the actual value doesn’t matter).
My patch script looks something like this
import capstone
import keystone
Cs = capstone.Cs(capstone.CS_ARCH_X86, capstone.CS_MODE_64)
Cs.detail = True
Ks = keystone.Ks(keystone.KS_ARCH_X86, keystone.KS_MODE_64)
with open('hopeanddreams.exe', 'rb') as f:
data = f.read()
copy_data = bytearray(data)
TEXT_FILE_OFFSET = 0x400
TEXT_FILE_SIZE = 0x466a00 - TEXT_FILE_OFFSET
TEXT_START = 0x140001000
def gen_nop(size):
match size:
case 1:
return b'\x90'
case 2:
return b'\x66\x90'
case 3:
return b'\x0f\x1f\x00'
case 4:
return b'\x0f\x1f\x40\x00'
case 5:
return b'\x0f\x1f\x44\x00\x00'
case 6:
return b'\x66\x0f\x1f\x44\x00\x00'
case 7:
return b'\x0f\x1f\x80\x00\x00\x00\x00'
case 8:
return b'\x0f\x1f\x84\x00\x00\x00\x00\x00'
case 9:
return b'\x66\x0f\x1f\x84\x00\x00\x00\x00\x00'
case _:
return b'\x66\x0f\x1f\x84\x00\x00\x00\x00\x00' + gen_nop(size - 9)
crefs = (
('cref_DAT_14047a3ac.txt', 0x14047a3ac),
('cref_DAT_14047a3b0.txt', 0x14047a3b0),
('cref_DAT_14047a3b4.txt', 0x14047a3b4),
)
for cref_file, cref_addr in crefs:
parsed_cref = []
with open(cref_file, 'rt') as f:
for line in f:
addr, _, _, _ = line.split('\t')
parsed_cref.append(int(addr, 16))
for addr in parsed_cref:
assert TEXT_START <= addr < TEXT_START + TEXT_FILE_SIZE
off = addr - TEXT_START + TEXT_FILE_OFFSET
insn = next(Cs.disasm(data[off:], addr, count=1))
assert insn.mnemonic == 'mov'
if insn.operands[0].type != capstone.x86.X86_OP_REG:
continue
assert insn.operands[1].type == capstone.x86.X86_OP_MEM
mem = insn.operands[1].mem
assert mem.base == capstone.x86.X86_REG_RIP
assert addr + insn.size + mem.disp == cref_addr
ass, l = Ks.asm(f'mov {insn.reg_name(insn.operands[0].reg)}, {0xdeadbeef ^ (cref_addr & 0xffffffff)}', addr=addr)
assert l == 1
assert len(ass) <= insn.size
if len(ass) < insn.size:
ass += gen_nop(insn.size - len(ass))
copy_data[off:off + insn.size] = ass
assert len(copy_data) == len(data)
with open('hopeanddreams.patched.exe', 'wb') as f:
f.write(copy_data)
Where I had the XREF locations exported from Ghidra and stored into separate files. If you know some Ghidra/IDA Pro scripting, you can probably do this programmatically, but I literally just copy-and-pasted.
However, this is not yet the end. You would realize that there are a lot of functions that look like this
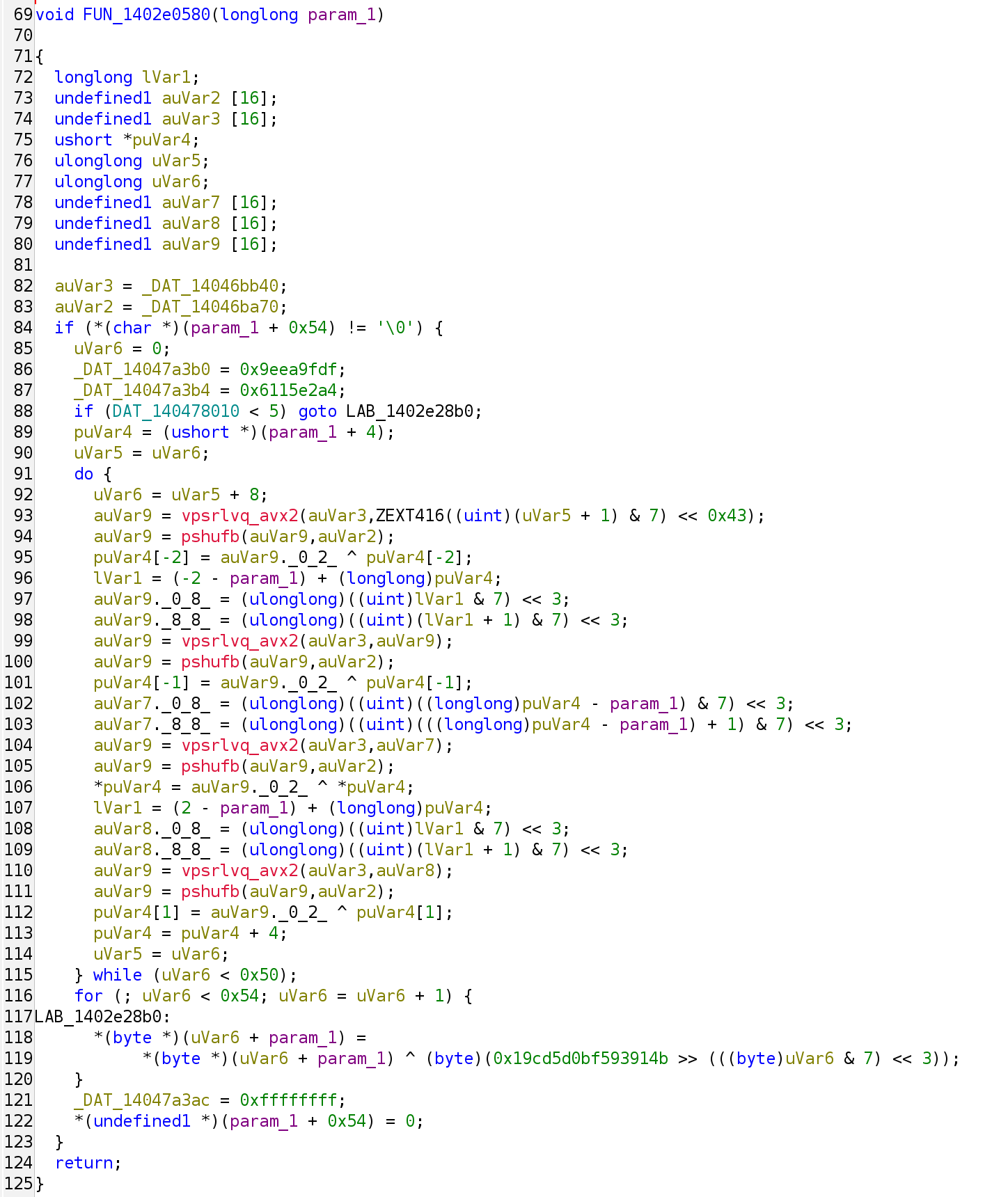
In fact, all string constants in the code are obfuscated through functions like this. Don’t worry if you see a bunch of non-decompilable AVX2 instructions, because it has a runtime CPU capability check (stored in 0x140478010) that falls back to a normal for loop if the CPU is incapable.
So we can easily see that this function essentially just does an XOR against a constant 0x19cd5d0bf593914b with the input bytes located in param_1. However, what is the actual address of the obfuscated string? It turns out there was another obfuscated function that does the address calculation:

The address turns out is stored inside the ThreadLocalStoragePointer, making it hard to recover in static analysis. angr in this case would also fall short because there is no easy way to correctly initialize the TLS pointer. Hence, the best way here is to use some kind of dynamic instrumentation tooling such as Frida or libdebug.
However, there is a trick without complex scripting, which is that most of the strings would have to go through FUN_1402cf1b0, which is a constructor of std::string from a const char *. Therefore, in my case, I just set a breakpoint there whenever I want to check what string is being used.
Static analysis
The code would contain a lot of stack variable assignments as seen already, but it’s easy to remove them with a regular expression replacement: ^\s+local_[a-f0-9]+ = (0x)?[a-f0-9]*;\n and ^\s+local_[a-f0-9]+ = local_[a-f0-9]+;\n to empty strings.
For example, the main function at 0x14020ba00 after cleaning up would look like this:
void FUN_14020ba00(void)
{
local_28 = DAT_140478040 ^ (ulonglong)auStack_488;
_DAT_14047a3b0 = 0x9eea1d5f;
_DAT_14047a3b4 = 0x9eea1d5b;
FUN_1402268c0(local_168,0x140);
FUN_14002e020(local_168,&DAT_1404780a0);
cVar1 = FUN_140081590(local_168);
if (cVar1 == '\0') {
_DAT_14047a3b0 = 0x9eea9fdf;
_DAT_14047a3b4 = 0x9eea78c9;
_DAT_14047a3ac = 0x9eea1d44;
local_283[0] = 0;
uVar2 = FUN_140226560(local_283);
uVar2 = FUN_14022e3d0(uVar2);
uVar2 = FUN_1402cf1b0(local_238,uVar2);
uVar3 = FUN_1402264d0(&local_284);
uVar3 = FUN_140230290(uVar3);
uVar3 = FUN_1402cf1b0(local_258,uVar3);
FUN_140054c50(uVar3,uVar2);
thunk_FUN_14042d3b0(local_258);
thunk_FUN_14042d3b0(local_238);
}
_DAT_14047a3b0 = 0x384b7e48;
_DAT_14047a3b4 = 0x8304;
_DAT_14047a3ac = 0x9eea1d43;
FUN_140036cf0(local_168,local_190);
uVar2 = FUN_140226640(&local_285);
uVar2 = FUN_14022c510(uVar2);
uVar2 = FUN_1402cf1b0(local_218,uVar2);
cVar1 = FUN_14042f6e0(local_190,uVar2);
thunk_FUN_14042d3b0(local_218);
if (cVar1 != '\0') {
_DAT_14047a3b0 = 0x384b7e48;
_DAT_14047a3b4 = 0x8304;
_DAT_14047a3ac = 0x9eea1d43;
uVar2 = FUN_140226700(&local_286,0);
uVar2 = FUN_140228790(uVar2);
uVar2 = FUN_1402cf1b0(local_1d8,uVar2);
uVar3 = FUN_1402266a0(&local_287);
uVar3 = FUN_14022a650(uVar3);
uVar3 = FUN_1402cf1b0(local_1f8,uVar3);
FUN_140054c50(uVar3,uVar2);
thunk_FUN_14042d3b0(local_1f8);
thunk_FUN_14042d3b0(local_1d8);
}
_DAT_14047a3ac = 0xffffffff;
FUN_140004080(local_198,8);
FUN_14000cf30(local_198,local_190);
cVar1 = FUN_1400d3e60(local_198,local_168);
if (cVar1 != '\0') {
_DAT_14047a3b4 = 0x9eea1d5b;
FUN_14012c6a0(local_198,local_168);
}
FUN_14000d630(local_198);
_DAT_14047a3ac = 0xffffffff;
_DAT_14047a3b4 = 0x6115e2a4;
thunk_FUN_14042d3b0(local_190);
FUN_1402267f0(local_168);
FUN_14044c220(local_28 ^ (ulonglong)auStack_488);
return;
}
Now it’s essentially code reading. You could use AI and dynamical debugging in the meantime to quickly locate the relevant parts and accelerate the process.
Essentially, there were three parts for communication:
First, handshake, which is handled in FUN_140081590. The client will first query locally the following information:
- Current date and time (up to hour)
- Machine name
- User name
Then <date_time><user_name>@<machine_name> is constructed and encrypted by the function FUN_140058a00:
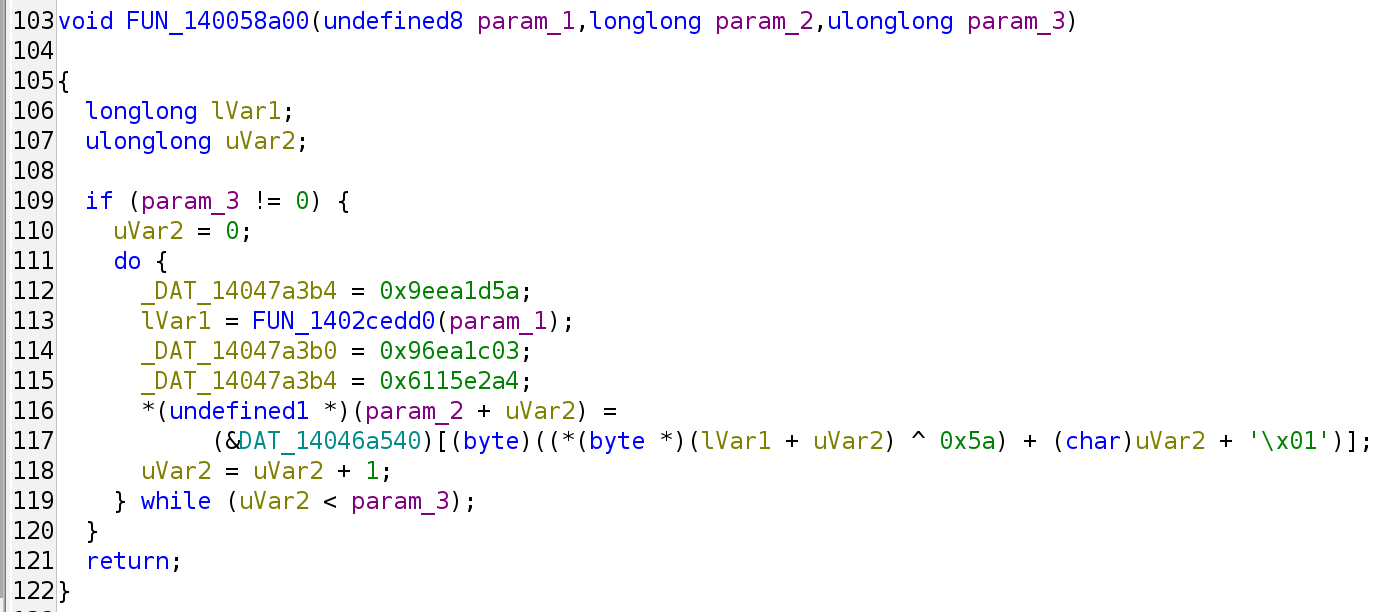
where the data inside 0x14046a540 is a classic substitution box. The function is equivalent to the following code:
def encrypt(s):
return bytes(mapping[((b ^ 0x5a) + i + 1) & 0xff] for i, b in enumerate(s))
Then an HTTP GET request is made to http://twelve.flare-on.com:8000/good with the encrypted string encoded into hex, embedded as Bearer Authorization token header. Using the request from the packet capture, we get that the original client was sending 2025082006TheBoss@THUNDERNODE.
By the way, library yhirose/cpp-httplib and nlohmann/json (3.12.0) are used in this program. You can find that out via debugging strings. You can quickly match the functions manually and rename them to better help with the reversing (or use some better technique like FLIRT).
The server replies a JSON, where there’s only a single d item. The value of the item is encrypted in a slightly different fashion, where the decrypting function is FUN_140066ba0.

The data inside 0x14047a390 is generated during program initialization, and is the inverse mapping of the above substitution box. Equivalently:
def decrypt_with_key(s, key):
return bytes(((inv_mapping[b] - 1 - i) & 0xff) ^ key[i % len(key)] for i, b in enumerate(s))
Where the key given is the <user_name>@<machine_name> sent to the remote.
After decryption we get the server handshake context:
{"sta": "excellent", "ack": "peanut@theannualtraditionofstaringatdisassemblyforweeks.torealizetheflagwasjustxoredwiththefilenamethewholetime.com:8080"}
For the second part, the function FUN_1400d3e60 would handle the communication hereafter, and a different encryption scheme is used. Inside the function FUN_140081300, a new shared secret is derived between the client and the server

where
- The inputs to the function are the same
<user_name>@<machine_name>sent in the first part, the username sent back from the serverack(in this case,peanut, the string before@), and the current hour (which should be the same as the datetime sent in the first part as well, but it’s actually re-acquired in the second part, so there’s a small edge case of being +1—not the case in this given pcap though). - The first parameter is passed through
FUN_140439850. From the internal constants, we can tell this is a SHA-256 hash function. Dynamically checking the input/output also confirms that. - The second and third parameter is concatenated together. In this case,
peanut06. - The concatenated string is passed through the same SHA-256 hash function.
- The result of two hashes are XOR’d together and returned.
In the specific case of the given packet capture, we have
SECRET_CLIENT = "TheBoss@THUNDERNODE"
SECRET_SERVER = "peanut" + "06"
SHARED_SECRET = SHA256(SECRET_CLIENT) ^ SHA256(SECRET_SERVER) = 95af8b095b7465f9059d0358bacc2238504059a0bd79b49b6790a6620add6d96
The result is then passed through function FUN_140050530, and subsequently FUN_1400500C0 which is clearly an AES Key Schedule function (seen from the operations and Rijndael S-box constants).
Then FUN_140050D20 is the actual AES encryption, where it splits the input into blocks of 16, initially XORs a buffer stored in param_1 + 0xf0, and then feeds into FUN_140050560 which contains 13+1 rounds of operations (corresponding to 256-bit key and therefore AES-256 is used). For the next block of 16 bytes, it XOR the output from the previous output, which indicates that this is using CBC block cipher mode, and consequently, param_1 + 0xf0 stores the Initialization Vector. Dumping it and we found that IV is simply 0x00, 0x01, ... 0x0f.
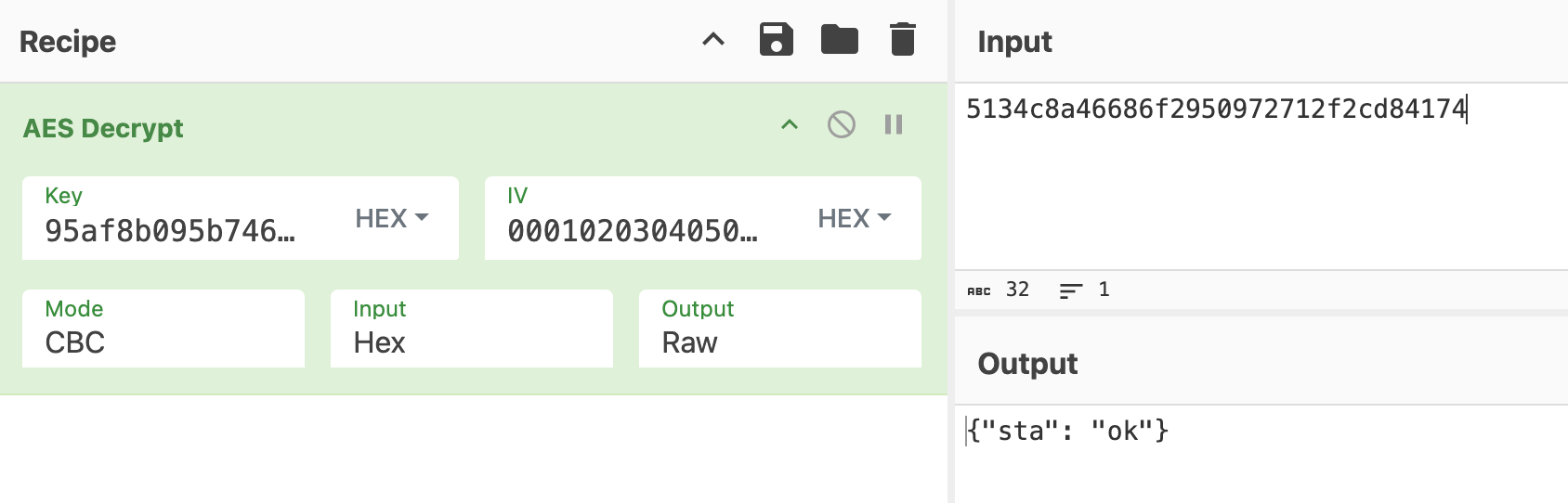
Using the AES cipher we can decrypt the first traffic after handshake:

And the server reply:
Unfortunately this is not the end yet. When you start decrypting the traffic, you inevitably encouter this one reply
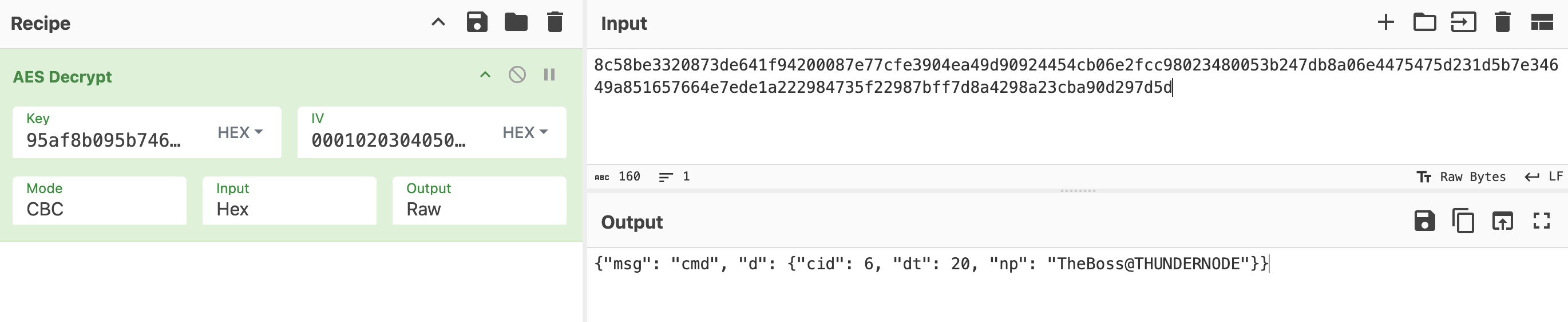
Which is located in the packet number 173 (or TCP stream 53). After this reply, suddenly the traffic is un-decryptable with the same cipher.
Something must have changed. Now, you could go ahead and actually reverse the whole thing, but here I took an educated guess that only the shared secret changed, but not the actual encryption scheme.
Dynamic analysis
So what I did was writing a simple server that implements what we know so far, and return the exact same message to trick the client into the path of renegotiating the shared secret, where I can set a breakpoint in the shared secret derivation function (FUN_140081300 as explained above). I see that the shared secret gets called, but this time the second parameter has been replaced by TheBoss@THUNDERNODE, which is the np value returned by the server. So the new shared secret becomes:
SECRET_CLIENT = "TheBoss@THUNDERNODE"
SECRET_SERVER = "TheBoss@THUNDERNODE" + "06"
SHARED_SECRET = SHA256(SECRET_CLIENT) ^ SHA256(SECRET_SERVER) = 848a5e071203cc8e8f476c25a3d1825fd5582ae7aaadd39bba70c994f9757cd9
And using the same AES scheme we can decrypt more traffic.
Then we are met with this giant payload in TCP stream 65:

After decryption we realized it is a ZIP file with password. We don’t have the password yet so let’s continue decrypting the traffic.
Then at packet number 232 (or TCP stream 68), we encountered yet another renegotiate shared secret command:

So we just have to recalculate again:
SECRET_CLIENT = "TheBoss@THUNDERNODE"
SECRET_SERVER = "miami" + "06"
SHARED_SECRET = SHA256(SECRET_CLIENT) ^ SHA256(SECRET_SERVER) = cf923be8da52631113752d5b32cef80b9d2bdadac85130811bee86868fe97204
And finally at TCP stream 74, we found the password:
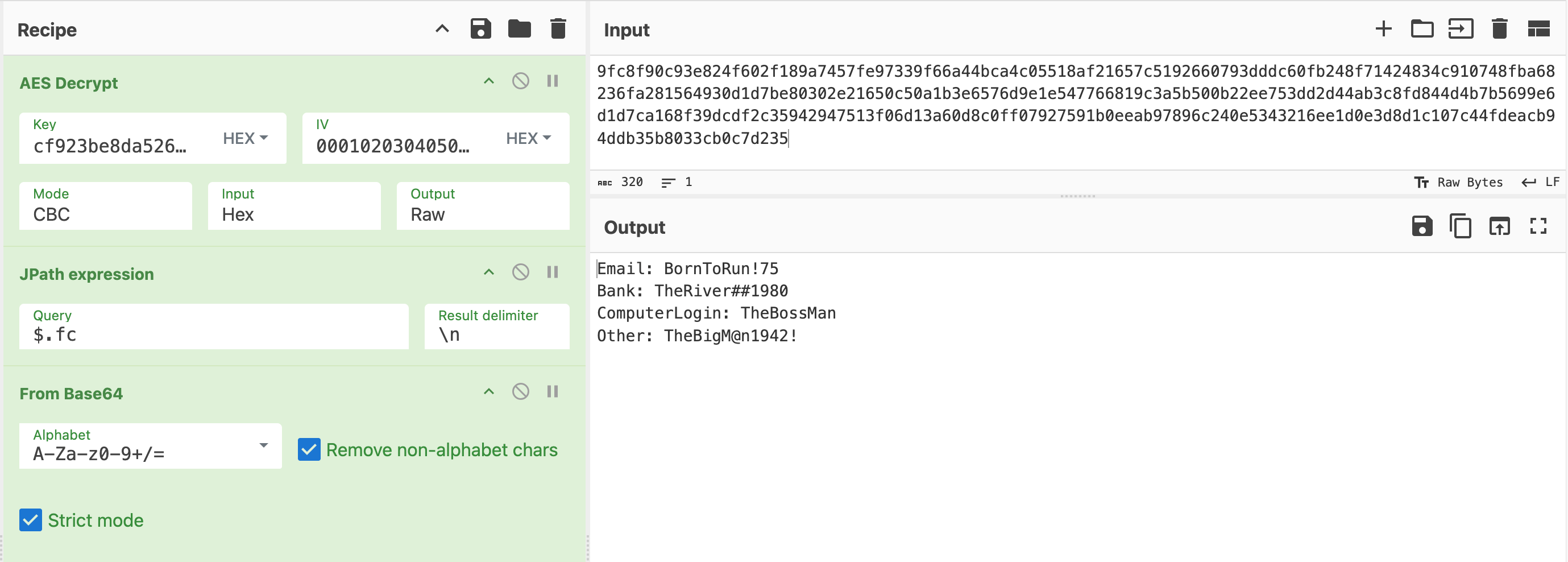
Using TheBigM@n1942! we can decrypt and decompress the ZIP file. Finally we get the flag image:

However, the author was too strict on the flag accept rule and I tried so many things but couldn’t get it accepted. Finally I have to uppercase
FLARE-ONbut lowercase.comto have the flag accepted…
8 – FlareAuthenticator
Another Windows executable. We are yet once again met with an obfuscated decompilation view with indirect calls, mixed boolean arithmetic, and indirect jumps.
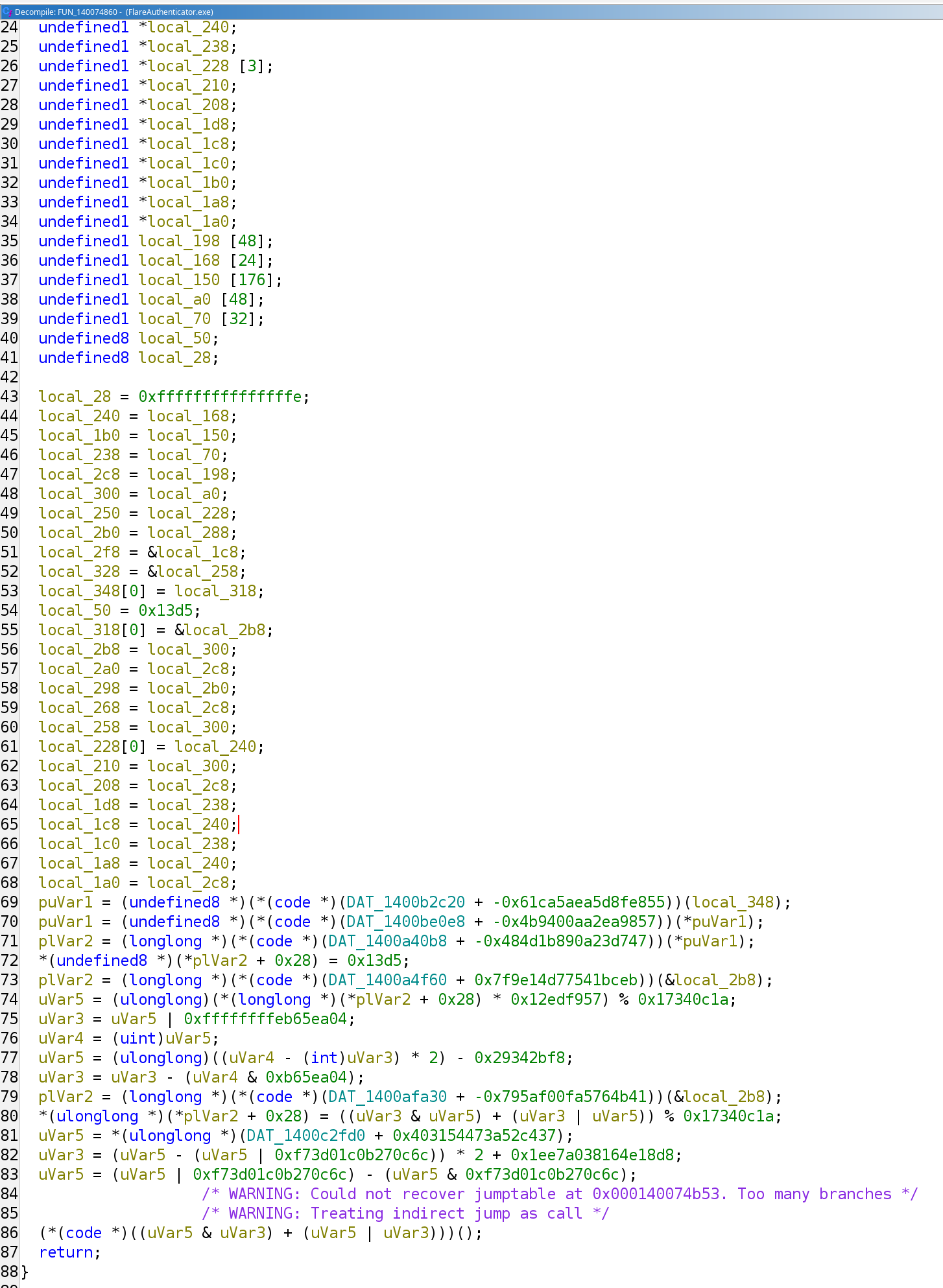
Deobfuscation
So first, we realize that there are a lot of function calls whose addresses are in the form of <data section value> + <constant>. In Ghidra, although the decompilation view doesn’t show you, the disassembly view actually performs constant propagation and calculates the actual address of the function call (!):
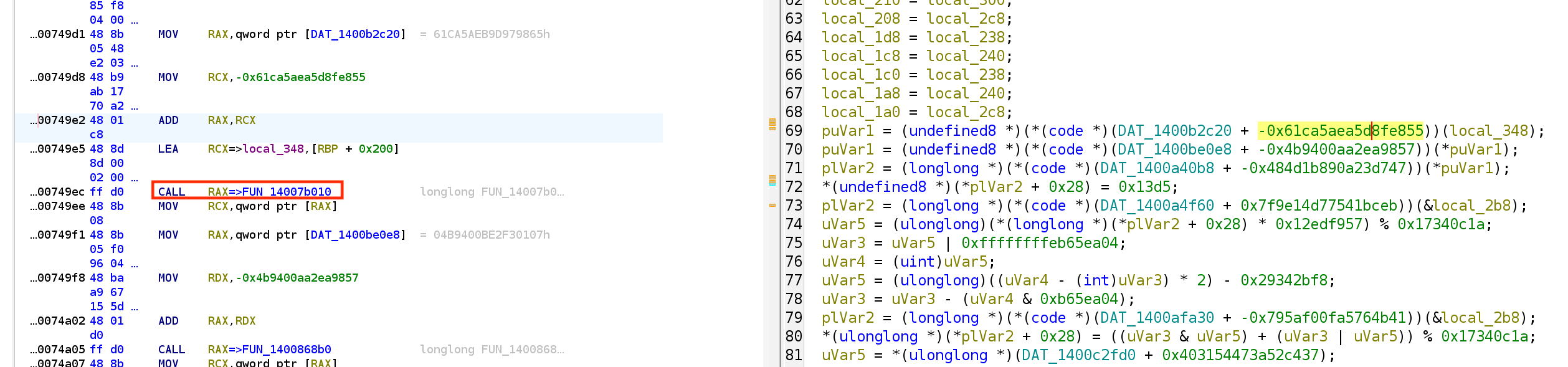
Now, the reason it doesn’t show in the decompiled view is because it is conservative on volatile memory changes. However, we could temporarily set the memory space to read-only for it to optimize via constant propagation:

And you can see we have recovered all function calls. Looking at one of these functions:
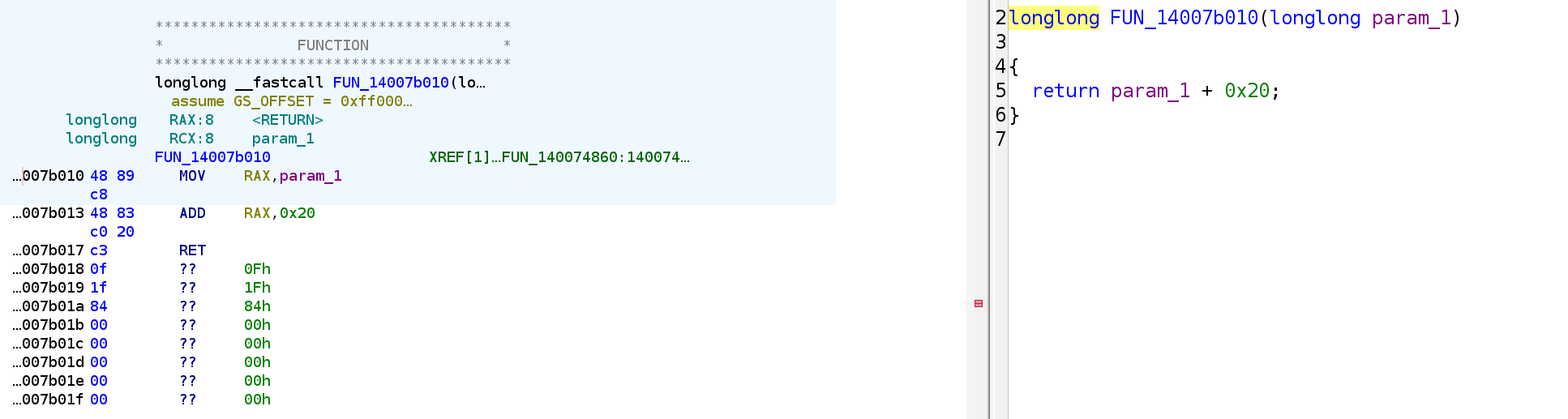
We realize most of these functions are very short ones that don’t even include prologue/epilogue. Therefore, if we could inline them at the call site, we could make our decompiled code way easier to read.
On the other hand, we noticed that the MBA part (bottom of the code, right before indirect jump) is also slightly more readable. We can just ask AI to simplify it for us:

Essentially, since bVar7 is a boolean (0 or 1), this is equivalent to:
if (bVar7) jmp_address = table[1] - 0x7bbf24faeb2e54fb;
else jmp_address = table[0] - (-0x7dbd9a4b6d1ff76a);
If we calculate the values ourselves, we get that the two branches are 0x140074c11 for false and 0x140075cc4 for true.
We followed these blocks and found that the remaining blocks have a similar structure to what we have seen above; therefore, for deobfuscation we need:
- Constant-propagate writable data section constants,
- Inline small function calls if possible, and
- Deobfuscate branching by converting MBA into normal expressions, and inline data section constants.
Luckily, they all have a very similar signature for us to pattern match as well.
For 1, we are matching blocks that look like this:

For 2, we need to write a heuristic for the caller function on whether to inline it or not. To inline it without worrying about too many edge cases, I have:
- The function must be a single block (i.e. no branching instructions other than a single
ret), - The function must have position-independent code only (i.e. no reference to RIP), and
- The function is small enough to be patched inline without relocating other instructions.
For 3, which is the most difficult part, we need to match something like this

And be able to extract all possible JMP destinations based on the relationship between RAX and RCX.
Since I can’t find an MBA deobfuscator that can act on machine code, I’m resorting to symbolic execution using angr (again). I could manually identify the start of such a block, run each instruction through until JMP is met, and then evaluate the result of RAX (jump destination) based on whether the initial condition is true or false. For example, if the initial SETcc is SETNZ, then after evaluation I can patch the instruction into JMPNZ <true_addr>; JMP <false_addr>.
There are a lot of other small cases that need to be handled, including CMOVcc and unconditional computed jumps, but they follow the same idea.
In the end, this is my patching script:
import itertools
import capstone
import claripy
import keystone
import angr
proj = angr.Project('FlareAuthenticator.exe', auto_load_libs=False)
Cs = capstone.Cs(capstone.CS_ARCH_X86, capstone.CS_MODE_64)
Cs.detail = True
Ks = keystone.Ks(keystone.KS_ARCH_X86, keystone.KS_MODE_64)
DATA_OFF = 0x9a800
DATA_SIZE = 0x2a800
DATA_BASE = 0x14009c000
TEXT_OFF = 0x400
TEXT_SIZE = 0x8d600
TEXT_BASE = 0x140001000
RDATA_OFF = 0x8da00
RDATA_SIZE = 0xce00
RDATA_BASE = 0x14008f000
with open('FlareAuthenticator.exe', 'rb') as f:
data = f.read()
def get_text(addr):
assert TEXT_BASE <= addr < TEXT_BASE + TEXT_SIZE, hex(addr)
off = addr - TEXT_BASE + TEXT_OFF
return data[off:]
def get_data(addr):
if RDATA_BASE <= addr < RDATA_BASE + RDATA_SIZE:
off = addr - RDATA_BASE + RDATA_OFF
return data[off:]
if DATA_BASE <= addr < DATA_BASE + DATA_SIZE:
off = addr - DATA_BASE + DATA_OFF
return data[off:]
return None
def get_insn(bytes, addr):
insns = tuple(Cs.disasm(bytes, addr))
assert len(insns) == 1
return insns[0]
def assem_insn(asm, addr):
b, l = Ks.asm(asm, addr=addr)
assert l == 1
return get_insn(bytes(b), addr)
def gen_nop(size):
match size:
case 1:
return b'\x90'
case 2:
return b'\x66\x90'
case 3:
return b'\x0f\x1f\x00'
case 4:
return b'\x0f\x1f\x40\x00'
case 5:
return b'\x0f\x1f\x44\x00\x00'
case 6:
return b'\x66\x0f\x1f\x44\x00\x00'
case 7:
return b'\x0f\x1f\x80\x00\x00\x00\x00'
case 8:
return b'\x0f\x1f\x84\x00\x00\x00\x00\x00'
case 9:
return b'\x66\x0f\x1f\x84\x00\x00\x00\x00\x00'
case _:
return b'\x66\x0f\x1f\x84\x00\x00\x00\x00\x00' + gen_nop(size - 9)
def emulate_br(addr, base_state=None):
if base_state is None:
state = proj.factory.blank_state(addr=addr, add_options={angr.options.SYMBOL_FILL_UNCONSTRAINED_REGISTERS})
else:
base_state.regs.rip = addr
state = base_state
simgr = proj.factory.simulation_manager(state)
pp = 0
for iid in range(100):
assert len(simgr.active) == 1
state = simgr.active[0]
cod = state.solver.eval_one(state.memory.load(state.addr, 16), cast_to=bytes)
insn = next(Cs.disasm(cod, state.addr, count=1))
if iid == 0:
assert insn.mnemonic.startswith('set')
simgr.step(num_inst=1)
assert len(simgr.active) == 1
state = simgr.active[0]
pp = state.regs.get(Cs.reg_name(insn.operands[0].reg))
continue
if insn.mnemonic == 'jmp':
assert insn.operands[0].type == capstone.x86.X86_OP_REG
assert insn.operands[0].reg == capstone.x86.X86_REG_RAX
solver = claripy.Solver()
solver.add(pp == 0)
zero_case = solver.eval(state.regs.rax, 2)
assert len(zero_case) == 1
zero_case = zero_case[0]
state.solver.add(pp != 0)
other_case = state.solver.eval_one(state.regs.rax)
assert zero_case != other_case
return zero_case, other_case
if 'mov' not in insn.mnemonic and insn.mnemonic not in ('lea', 'neg', 'or', 'add', 'and', 'sub', 'shl'):
raise Exception(f'Unexpected instruction: {insn} @ {hex(addr)}')
simgr.step(num_inst=1)
raise Exception('Too many instructions')
def emulate_jmp(addr):
state = proj.factory.blank_state(addr=addr, add_options={angr.options.SYMBOL_FILL_UNCONSTRAINED_REGISTERS})
simgr = proj.factory.simulation_manager(state)
for _ in range(100):
assert len(simgr.active) == 1
state = simgr.active[0]
insn = next(Cs.disasm(get_text(state.addr), state.addr, count=1))
if insn.mnemonic == 'jmp':
assert insn.operands[0].type == capstone.x86.X86_OP_REG
assert insn.operands[0].reg == capstone.x86.X86_REG_RAX
return state.solver.eval_one(state.regs.rax)
if 'mov' not in insn.mnemonic and insn.mnemonic not in ('lea', 'or', 'add', 'and', 'sub', 'neg'):
raise Exception(f'Unexpected instruction: {insn} @ {hex(addr)}')
simgr.step(num_inst=1)
raise Exception('Too many instructions')
def emulate_cmov(addr, type):
state = proj.factory.blank_state(addr=addr, add_options={angr.options.SYMBOL_FILL_UNCONSTRAINED_REGISTERS})
b, l = Ks.asm(f'set{type} cl')
assert l == 1
state.memory.store(addr - len(b), bytes(b))
return emulate_br(addr - len(b), base_state=state)
deobfsted = set()
def extract_insns(addr, space):
insns = []
for insn in Cs.disasm(get_text(addr), addr):
if insn.mnemonic == 'jmp':
assert not insns, hex(addr)
return None
insns.append(insn)
space -= insn.size
if space < 0:
return None
if insn.mnemonic == 'ret':
break
assert insns.pop().mnemonic == 'ret'
return insns
def deobf_run(target):
if target in deobfsted:
return
deobfsted.add(target)
insns = []
for insn in Cs.disasm(get_text(target), target):
insns.append(insn)
if insn.mnemonic in ('ret', 'jmp', 'int1'):
break
the_end = insns[-1].address + insns[-1].size
idx = 0
processed = []
while idx < len(insns):
insn = insns[idx]
for _ in (None, ):
if insn.mnemonic.startswith('j'):
assert insn.operands[0].type == capstone.x86.X86_OP_IMM, insn
dest = insn.operands[0].imm
yield from deobf_run(dest)
continue
if insn.mnemonic in ('setne', 'sete', 'setge'):
nxt_insn = insns[idx + 1]
if nxt_insn.mnemonic == 'mov':
if nxt_insn.operands[0].type != capstone.x86.X86_OP_REG:
continue
if nxt_insn.operands[1].type != capstone.x86.X86_OP_MEM:
continue
if nxt_insn.operands[1].mem.base != capstone.x86.X86_REG_RIP:
continue
elif nxt_insn.mnemonic == 'movzx':
assert nxt_insn.operands[0].type == capstone.x86.X86_OP_REG
assert nxt_insn.operands[1].type == capstone.x86.X86_OP_REG
assert nxt_insn.operands[1].reg == insn.operands[0].reg
else:
continue
zero_case, other_case = emulate_br(insn.address)
new_insn = assem_insn(f'j{insn.mnemonic[3:]} {hex(other_case)}', insn.address)
new_insn2 = assem_insn(f'jmp {hex(zero_case)}', new_insn.address + new_insn.size)
processed.append(new_insn)
processed.append(new_insn2)
print('converted 3:', insn, '->', new_insn, new_insn2)
yield from deobf_run(zero_case)
yield from deobf_run(other_case)
idx = float('inf')
break
if insn.mnemonic != 'mov':
continue
if insn.operands[0].type != capstone.x86.X86_OP_REG:
continue
if insn.operands[1].type == capstone.x86.X86_OP_IMM:
nxt_insn = insns[idx + 1]
if nxt_insn.mnemonic != 'mov':
continue
if nxt_insn.operands[0].type != capstone.x86.X86_OP_REG:
continue
if nxt_insn.operands[1].type != capstone.x86.X86_OP_IMM:
continue
nxt2_insn = insns[idx + 2]
if not nxt2_insn.mnemonic.startswith('cmov'):
continue
if nxt2_insn.operands[0].type != capstone.x86.X86_OP_REG:
continue
if nxt2_insn.operands[1].type != capstone.x86.X86_OP_REG:
continue
if nxt2_insn.operands[0].reg != nxt_insn.operands[0].reg:
continue
if nxt2_insn.operands[1].reg != insn.operands[0].reg:
continue
zero_case, other_case = emulate_cmov(insn.address, nxt2_insn.mnemonic[4:])
new_insn = assem_insn(f'j{nxt2_insn.mnemonic[4:]} {hex(other_case)}', insn.address)
new_insn2 = assem_insn(f'jmp {hex(zero_case)}', new_insn.address + new_insn.size)
processed.append(new_insn)
processed.append(new_insn2)
print('converted 4:', insn, '->', new_insn, new_insn2)
yield from deobf_run(zero_case)
yield from deobf_run(other_case)
idx = float('inf')
break
if insn.operands[1].type != capstone.x86.X86_OP_MEM:
continue
if insn.operands[1].mem.base != capstone.x86.X86_REG_RIP:
continue
if insn.operands[1].mem.index != 0:
continue
if insn.operands[1].mem.scale != 1:
continue
data_imm = int.from_bytes(get_data(insn.address + insn.size + insn.operands[1].mem.disp)[:insn.operands[0].size], 'little')
nxt_insn = insns[idx + 1]
if nxt_insn.mnemonic != 'movabs':
continue
if nxt_insn.operands[0].type != capstone.x86.X86_OP_REG:
continue
if nxt_insn.operands[1].type != capstone.x86.X86_OP_IMM:
continue
nxt2_insn = insns[idx + 2]
if nxt2_insn.mnemonic in ('add', 'sub'):
if nxt2_insn.operands[0].type != capstone.x86.X86_OP_REG:
continue
if nxt2_insn.operands[1].type != capstone.x86.X86_OP_REG:
continue
if nxt2_insn.operands[0].reg != insn.operands[0].reg:
continue
if nxt2_insn.operands[1].reg != nxt_insn.operands[0].reg:
continue
reloc = []
bailed = False
for iid in range(100):
if insns[idx + 3 + iid].mnemonic == 'call':
idx += 3 + iid
break
if insns[idx + 3 + iid].mnemonic in ('jmp', 'ret'):
bailed = True
break
if insns[idx + 3 + iid].mnemonic == 'mov' \
and insns[idx + 3 + iid].operands[0].type == capstone.x86.X86_OP_REG \
and insns[idx + 3 + iid].operands[0].reg == capstone.x86.X86_REG_RAX:
bailed = True
break
reloc.append(insns[idx + 3 + iid])
else:
raise Exception('wtf')
if bailed:
continue
assert insns[idx].operands[0].type == capstone.x86.X86_OP_REG
assert insns[idx].operands[0].reg == capstone.x86.X86_REG_RAX
# print(insns[idx], insn, nxt_insn)
idx += 1
if nxt2_insn.mnemonic == 'add':
total = (data_imm + nxt_insn.operands[1].imm) & 0xffff_ffff_ffff_ffff
else:
total = (data_imm - nxt_insn.operands[1].imm) & 0xffff_ffff_ffff_ffff
avail_space = insns[idx].address - insn.address
for r in reloc:
avail_space -= r.size
exted = extract_insns(total, avail_space)
if exted is not None:
reloc.extend(exted)
now = insn.address
for r in reloc:
for op in r.operands:
if op.type == capstone.x86.X86_OP_MEM:
assert op.mem.base != capstone.x86.X86_REG_RIP
assert op.mem.index != capstone.x86.X86_REG_RIP
new_r = get_insn(r.bytes, now)
assert new_r.op_str == r.op_str
now += r.size
# print(new_r)
processed.append(new_r)
if exted is None:
processed.append(assem_insn(f'call {hex(total)}', now))
else:
if len(nxt2_insn.operands) != 2:
continue
called = False
for sc in range(100):
if insns[idx + 2 + sc].mnemonic == 'jmp':
break
elif insns[idx + 2 + sc].mnemonic in ('call', 'ret'):
called = True
break
if called:
if nxt2_insn.mnemonic != 'mov':
continue
if nxt2_insn.operands[1].type != capstone.x86.X86_OP_MEM:
continue
if nxt2_insn.operands[1].mem.base != insn.operands[0].reg:
continue
if nxt2_insn.operands[1].mem.index != nxt_insn.operands[0].reg:
continue
if nxt2_insn.operands[1].mem.scale != 1:
continue
if nxt2_insn.operands[1].mem.disp != 0:
continue
total = (data_imm + nxt_insn.operands[1].imm) & 0xffff_ffff_ffff_ffff
gd = get_data(total)
if gd is None:
continue
act = int.from_bytes(gd[:nxt2_insn.operands[1].size], 'little')
nin = assem_insn(f'mov {nxt2_insn.op_str.split(",")[0]}, {act}', insn.address)
processed.append(nin)
print('converted 2 (old):', insn, nxt_insn, nxt2_insn, '->', nin)
idx += 3
break
print(insn, nxt_insn, nxt2_insn)
dest = emulate_jmp(insn.address)
new_insn = assem_insn(f'jmp {hex(dest)}', insn.address)
processed.append(new_insn)
print('converted 2:', insn, '->', new_insn)
yield from deobf_run(dest)
idx = float('inf')
break
else:
processed.append(insn)
idx += 1
code = bytearray()
current = target
for insn in processed:
if insn.address != current:
assert insn.address > current, insn
code += gen_nop(insn.address - current)
current = insn.address
code += insn.bytes
current += len(insn.bytes)
assert current <= the_end
assert len(code) <= the_end - target
yield target, code
def main():
deobf = itertools.chain(deobf_run(0x1400202b0), deobf_run(0x14005ef60), deobf_run(0x140012e50), deobf_run(0x140081760))
patched = []
n_data = data
for off, code in deobf:
for po, pl in patched:
if off < po + pl and po < off + len(code):
print(f'overlap: {hex(off)}-{hex(off+len(code))} vs {hex(po)}-{hex(po+pl)}')
assert off+len(code) == po+pl
patched.append((off, len(code)))
assert TEXT_BASE <= off < TEXT_BASE + TEXT_SIZE
n_data = (n_data[:off - TEXT_BASE + TEXT_OFF] +
code +
n_data[off - TEXT_BASE + TEXT_OFF + len(code):])
assert len(n_data) == len(data)
with open('FlareAuthenticator.patched.exe', 'wb') as f:
f.write(n_data)
if __name__ == '__main__':
main()
The resulting main function would look something like this:
It is still quite unreadable, but at least all the function calls are clear. So we can start doing analysis.
Dynamic + static analysis
The main window of the application looks like this:
And if we input 25 letters, the “OK” button becomes available. If we press it, we get
Unfortunately, this Wrong Password string is nowhere to be found in the binary. However, we know that this program is using Qt, and this popup feels really like Qt’s default QMessageBox::warning. Therefore, we set breakpoints at all versions of this function

And behold, we indeed got a hit
Then we can just look at the call stack trace to figure out what is the actual handler function for validating the input
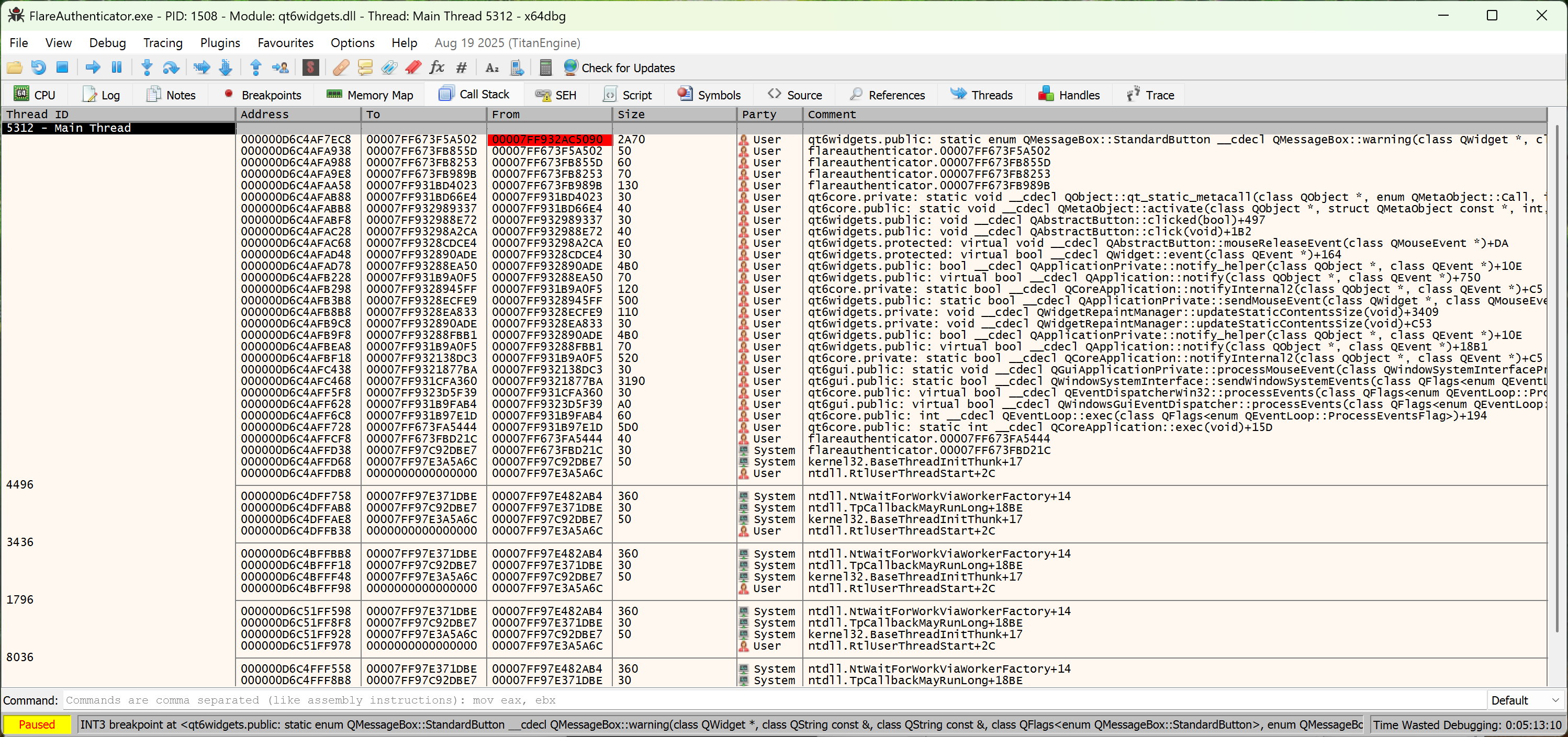
The second-to-last frame brings us to FUN_1400202b0. Again, even after deobfuscation the method looks unreadable. However, AI would be of great help here:
Turns out, the OK button just does a constant check against a hardcoded constant. The actual calculation must be done somewhere else. To figure it out, let’s first see how this value is changed depending on the input. We set a breakpoint at 0x140021E29 where the dynamic value is dereferenced.
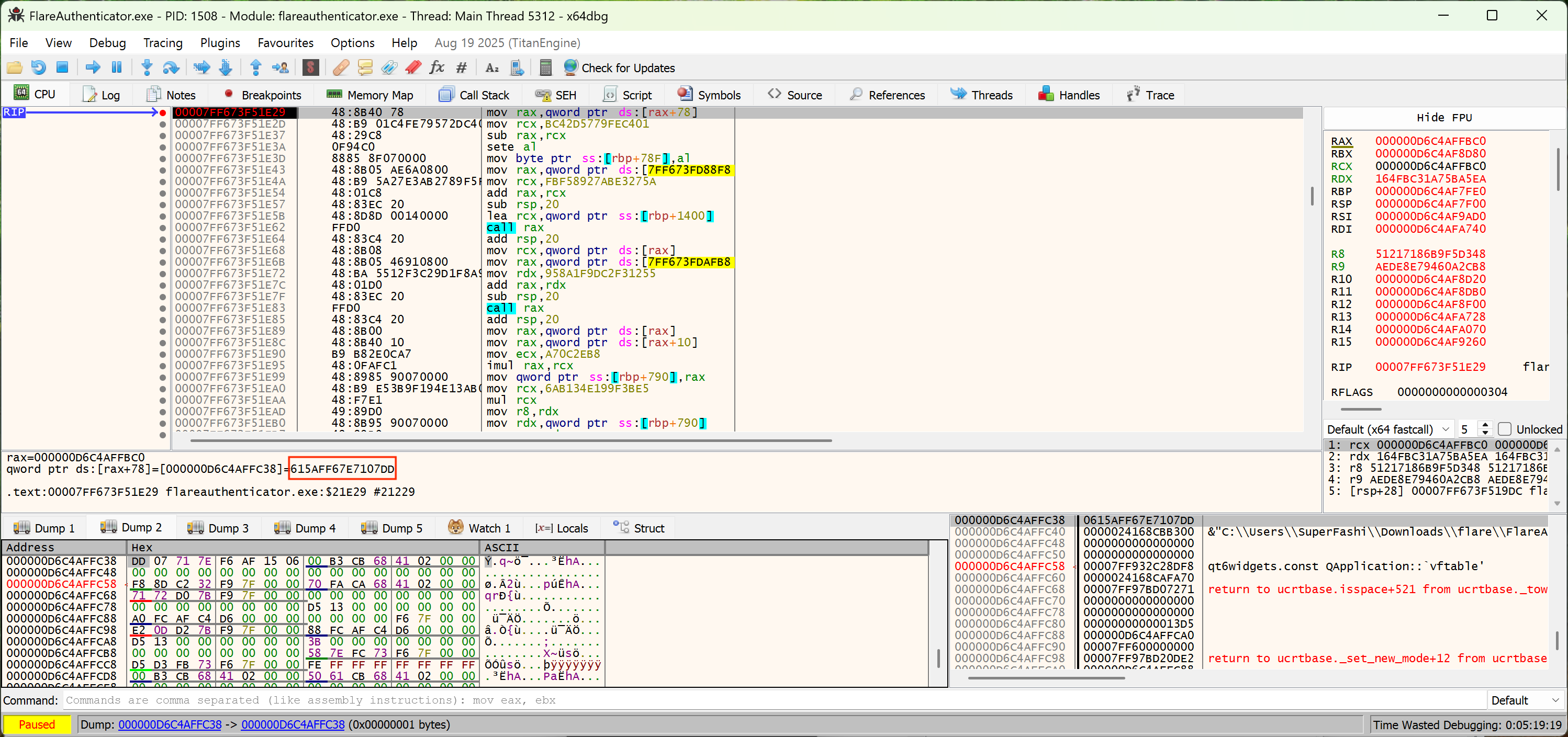
When the input is full of 1s, this value is retrieved and compared against the hardcoded constant. After some testing, we conclude the following:
- Given the input of 25 bytes, the same input would result in the same
uint64value. - The calculation has an avalanche effect (i.e., changing only one byte would cause this value to change drastically).
- Furthermore, the memory location of this value does not change every time.
The last point is good news for us, because that means we can monitor the changes regarding the input. So we just keep this memory address inside the view of the dump and do more testing while inputting the numbers. We noticed more:
- The value would be fully
0at the very beginning. - Whenever a digit is pressed (a number is entered), the value would change.
- Whenever “DEL” is pressed, the value would also change, and it would change back to the previous value.
This confirms that our target is to figure out the correct 25 inputs that make the value equal to the expected value.
The above investigation also implies that we can use the advanced technique of setting a hardware breakpoint whenever this value is modified, so we can directly trace to the specific instruction that does the calculation.
When we press a digit button, we break at this address with the following call stack:
The top stack frame correspond to the function at 0x140012E50. So we do the same thing of asking our Claude-senpai:

The important code recovered by AI is over here:
// Get current input count
__int16 currentCount = *(_QWORD *)(a1 + 104);
// Calculate some value based on button and current state
__int64 baseValue = sub_140081760(a1, currentCount);
// Get another text copy for character processing
QString anotherTextCopy;
QAbstractButton::text(buttonValue, &anotherTextCopy);
QByteArray anotherUtf8;
QString::toUtf8(&anotherTextCopy, &anotherUtf8);
// Get first character and do some calculation
char firstChar = QByteArray::at(&anotherUtf8, 0);
__int64 shiftedCount = *(_QWORD *)(a1 + 104) << someShiftAmount; // Complex shift calculation was obfuscated
// Calculate some combined value
__int64 combinedValue = sub_140081760(a1, firstChar + shiftedCount) * baseValue;
// Update the accumulator/total
*(_QWORD *)(a1 + 120) += combinedValue;
Essentially, for each digit we input, depending on the position, we have the following two values
v1 := sub_140081760(a1, <index>)
v2 := sub_140081760(a1, (<index> << someShiftAmount) + <input>)
And the value accumulated onto the final result value is v1 * v2.
AI couldn’t figure out what that shift amount is because of the obfuscation; however, we can find it out pretty easily by simply setting a breakpoint at sub_140081760 and looking at the relationship of the input values.
For example, when we press digit 1 in the 2nd place, sub_140081760 is called twice where we see
sub_140081760(<...>, 0x0002)
sub_140081760(<...>, 0x0231)
So we conclude that
- The index is 1-based,
- The shift amount is 8, and
- The input is given as ASCII
However, when we try to do the same thing to sub_140081760 where we ask Claude what is it doing, it couldn’t figure out the correct answer anymore.
After some more manual analysis, we realized that sub_140081760 is pure (and in fact, does not use the first argument at all). This means it can be taken as a black box that converts a uint16 number into a uint64 number.
Furthermore, the number of possible inputs is very limited. We only have the positional possibility from 1 to 25, and the input possibility from 0x30 to 0x39 (ASCII 0 to 9). That means we just need to query all possible cases to get the mapping.
You can do this by dynamic instrumentation or emulation. For me I chose angr:
import angr
import claripy
proj = angr.Project('FlareAuthenticator.exe', auto_load_libs=False)
def calc(inp):
assert inp.length == 16
call = proj.factory.callable(0x140081760, prototype='uint64_t func(void *, uint16_t)', add_options={angr.options.ZERO_FILL_UNCONSTRAINED_REGISTERS})
res = call(0, inp)
return res
options = [[] for _ in range(25)]
for i in range(1, 26):
for j in range(ord('0'), ord('9') + 1):
py = claripy.Concat(claripy.BVV(i, 8), claripy.BVV(j, 8))
assert py.size() == 16
l = calc(claripy.BVV(i, 16))
r = calc(py)
options[i - 1].append((l * r).concrete_value)
Once we extracted all possible cases, the remaining was a knapsack problem (integer linear programming). Z3 is obviously the best at solving this kind of NP-complete problem (exact and under modulo):
TARGET = 0x0BC42D5779FEC401
solver = z3.Solver()
sums = [z3.BitVec(f'sum{i}', 64) for i in range(25)]
summ = sum(sums)
for i in range(25):
solver.add(z3.Or([sums[i] == v for v in options[i]]))
solver.add(summ == TARGET)
print('solving...')
assert solver.check() == z3.sat
model = solver.model()
for i, s in enumerate(sums):
print(chr(options[i].index(model[s].as_long()) + ord('0')), end='')
print()
We get that the answer is 4498291314891210521449296. Input it and we get the flag.
Bonus time!
What is the actual calculation inside sub_140081760, you ask? Spoiler alert, it is this:
def calc(num):
x = ZeroExt(16, num)
y = LShR(x, 0x10)
a = x ^ 0x3d
b = a ^ y
c = b << 3
d = b + c
e = LShR(d, 4)
f = d ^ e
h = 0x27d4eb79 * f
g = LShR(h, 0xf)
res = LShR(g ^ h, 4)
return ZeroExt(32, res)
To figure it out without painstaking reversing and deobfuscation, we need to use the power of symbolic execution and program synthesis. This topic is truly worthy of another write-up, so we’ll leave it for a later time.
9 – 10000
We are given a humongous Windows executable. However, opening it in IDA Pro, we don’t see that much code. Going to the main function at sub_140001E87, we see rather straightforward, non-obfuscated code.

Static analysis (with AI)
Let’s ask AI to make an analysis for us.

With some more queries, it gives us a nice and basically correct summary of what the main function does:
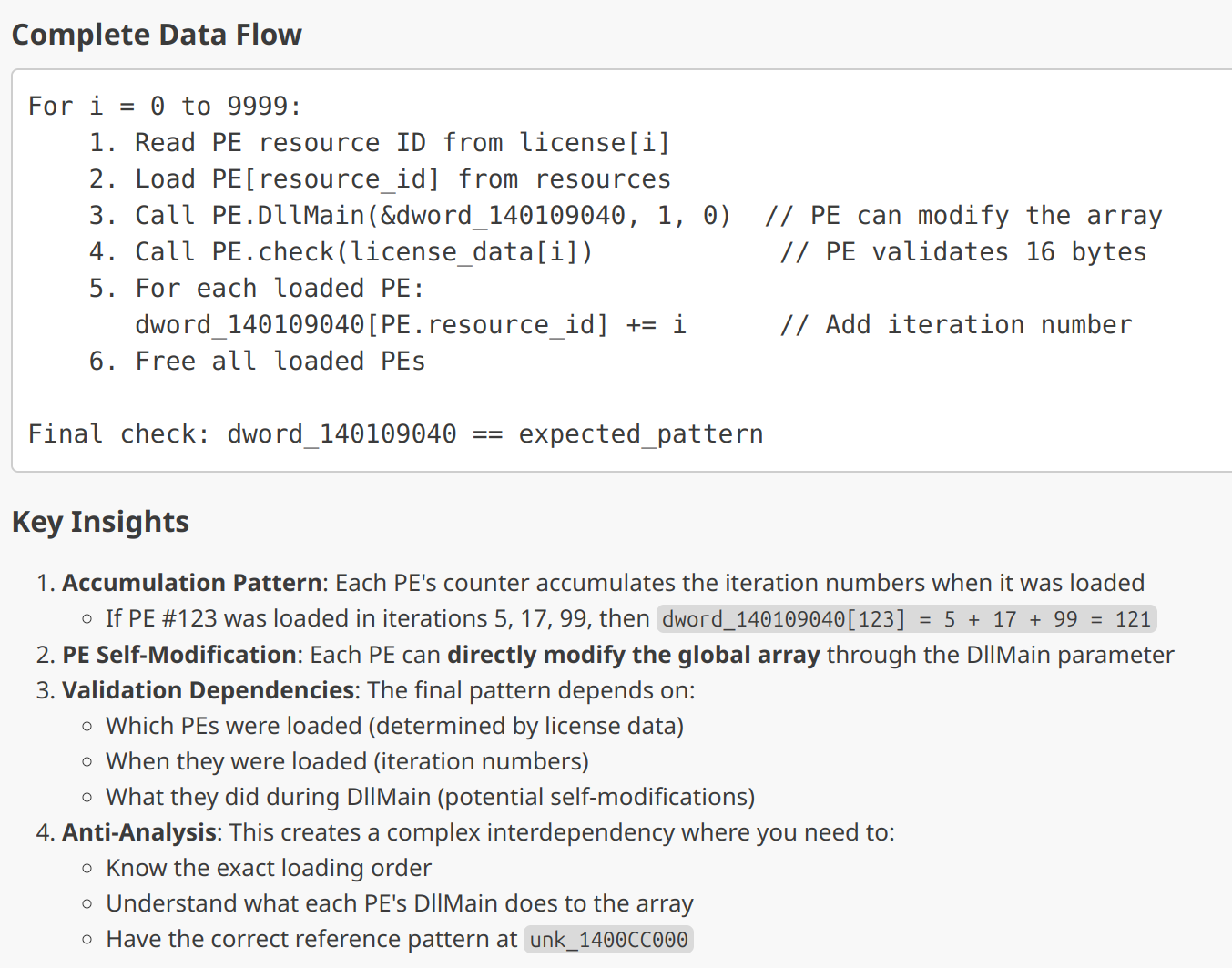
Summarize again here:
- The challenge reads in a file called
license.bin. - There are PE files inside the executable resources.
- The license file is parsed so that there are 10000 entries. Each entry contains a resource ID to load from, and 32 bytes (AI mistook 16
uint16_tas 16 bytes) of input to validate. - For each entry, the PE file corresponding to that resource is loaded.
- The PE file is initialized with the same arguments through its entry point
DllMain, with the counter array located at0x140109040as the argument. - The PE file’s
_Z5checkPh(which demangles tocheck(unsigned char*)) is called with the 32-byte input as the argument. - After each
check, the counter array for each loaded PE is incremented by the current loop count. - The target is to make each
checkvalidation pass and the final counter array equal a constant stored at0x1400CC000.
First, I decided to extract all resources and see what each PE file looks like. The normal tool ResourceHacker actually freezes when trying to open this program (probably because there are too many large resource files), so I used this tool folbricht/pefile to extract all resources programmatically.
After extraction, somehow the data extracted is not an executable. Opening it up in a hex viewer, we see something like this instead:
Although not following the format of a PE file, it is very clear that it should be one, as strings like “This program[…]” are contained in the file. So the file must have gone through some kind of non-cryptographic encoding.
The AI result above actually mentioned decompression/unpacking. It says that it is using Snappy as the compression method, but existing tools to decompress Snappy data do not work. So I had to ask again:

AI changed its idea to something called aPLib. After some testing, I found this existing Python code snemes/aplib that can do the decompression with no issue. So now we can finally take a look at all these 10000 PE files.
Somehow IDA has issues with the calling convention. Although automatic fixing is probably possible through scripts, we are switching to Ghidra again.

At the beginning of the function was a bunch of function calls. Some of these functions are in the same PE file, but some of these functions (the ones in red) are actually externs/imports that are found in other PE files (in the resource). Let’s call them f functions.
Then if we scroll down, after the f function calls, we have this huge chunk of code that is doing some kind of calculation:

Then finally, the result is checked against a constant buffer in the binary:
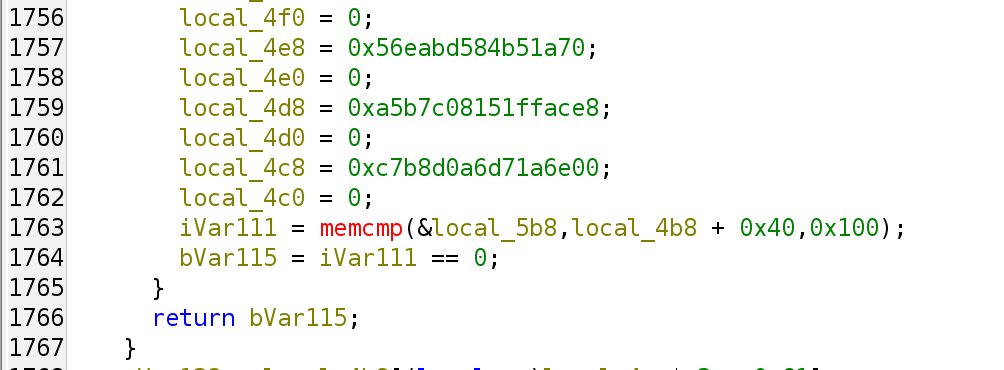
If it matches, the validation passes.
We could check a few more different PE files and confirm that they all have basically the same structure.
You know that whenever something like this appears, I resort to angr. So I quickly wrote something like this:
import angr
import claripy
proj = angr.Project('dlls/0000.dll', auto_load_libs=False)
check_addr = proj.loader.find_symbol('_Z5checkPh').rebased_addr
base_state = proj.factory.blank_state(add_options={angr.options.ZERO_FILL_UNCONSTRAINED_REGISTERS})
arg = base_state.heap.allocate(0x10)
inp = claripy.BVS('inp', 8 * 0x10)
base_state.memory.store(arg, inp)
print('running check')
check = proj.factory.callable(check_addr, prototype='uint8_t check(uint8_t*)', add_options={angr.options.ZERO_FILL_UNCONSTRAINED_REGISTERS}, base_state=base_state)
ret = check(arg)
print(ret)
However, we are met with the following warning:
WARNING | 2025-10-24 16:54:30,752 | angr.storage.memory_mixins.default_filler_mixin | Filling memory at 0x0 with 4 unconstrained bytes referenced from 0x22415f682 (_Z21f38236877289593244403Ph+0x1c in 0000.dll (0x22415f682))
This happened in one of those f functions which we haven’t checked yet. So let’s take a look.
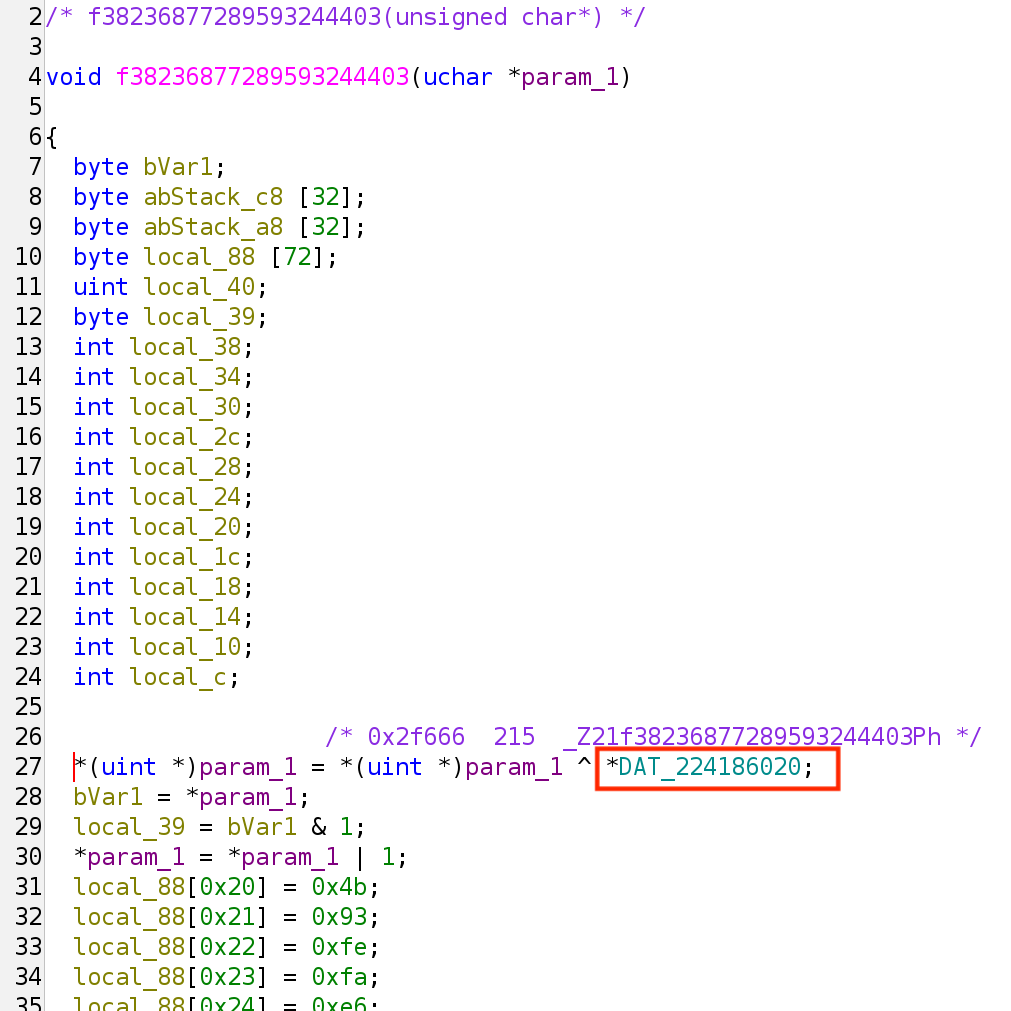
As you can see, it tries to dereference a pointer value at 0x224186020, but it doesn’t have an initial value. Looking for cross-references to this location, we see that it is written only in this function FUN_22417e428:
And if we trace this all the way back, we realize this value is actually passed all the way through from the entry point’s first argument, which is exactly the counter array that the AI analyzed.
Therefore the counter array is involved in the computation itself. Without figuring out the counter array values, it would probably be very difficult to proceed, so let’s do that first.
Counter array
As analyzed by AI
- There is a particular order of the PE (DLL) files that is loaded, that is indicated in the given license file.
- When each PE is loaded, all its imported DLLs would be loaded, and recursively so.
- After each execution of
check, the counter array is updated, where for all PE files that are loaded, their respective resource ID index in the counter array would be increased by the current loop iteration count (we’ll call it the “round number” from now on). - The loaded PE list is reset and the process is repeated for the next license entry.
This sounds very complicated, but hopefully the pseudo-code is easier to understand:
type License:
uint16_t resource_id
uint8_t data[32]
type Resource:
uint16_t resource_id
uint16_t import_resource_ids[]
License licenses[10000]
uint64_t counter[10000]
Resource pes_loaded[]
def load_pe(resource_id):
if resource_id in any of pes_loaded:
return
# load pe from resources by id
resource = load_resource(resource_id)
pes_loaded.append(resource)
for i in import_resource_ids:
load_pe(i)
for i, l in enumerate(licenses):
load_pe(l.resource_id)
# initialize DLL with counter array
# call check(l.data)
for res in pes_loaded:
counter[res.resource_id] += i
pes_loaded.clear()
There are two other important points that we haven’t mentioned
- Each resource can only be in the license file once (this is checked in
sub_140028F80). In other words, the license file should contain the full set of resource IDs, but potentially shuffled. - Each PE (DLL)
checkfunction only reads the counter array, but do not modify it.
Therefore, if we can figure out the order of resource IDs in the license file, then we can simulate this process and reconstruct the counter array values that is used in the check functions.
However, the only thing we know is the final state of the counter array, which is the data stored in 0x1400CC000. To use it to restore the original order, we need some graph theory knowledge.
For the following, I’m using PE file
X, resource fileX, and a node \(X\) in the dependency graph interchangeably.
If we see each PE file as a single node in a graph, and see PE file A importing a function from PE file B as there’s an edge from \(A\) to \(B\), then we get what’s so called a dependency graph. In this graph, if there’s a path from node \(X\) to node \(Y\), then it means when PE file X is loaded, Y must also be loaded.
Let’s first construct such a graph. Using pefile:
import pefile
from collections import defaultdict
graph = defaultdict(list)
for i in range(10000):
path = f'dlls/{i:04d}.dll'
pe = pefile.PE(path)
for entry in pe.DIRECTORY_ENTRY_IMPORT:
assert entry.dll.endswith(b'.dll')
name = entry.dll[:-4]
if name.isdigit():
assert len(name) == 4
idx = int(name)
graph[i].append(idx)
Here, the graph is stored in a format called adjacency list.
The very first thing we want to make sure is that this graph is acyclic. If not, it will be way harder to reason about later and some strongly connected components stuff have to come out. To do this, we can use a Depth-First Search.
def dfs(node, visiting):
if node in visiting:
assert not visiting[node], 'cycle detected'
return
visiting[node] = True
for n in graph.get(node, ()):
dfs(n, visiting)
visiting[node] = False
visiting = dict()
for i in range(10000):
dfs(i, visiting)
This guarantees us that no cycle exists in the dependency graph.
The first important theorem we can derive from everything we know so far is,
- The tree rooted at a node \(X\) (or equivalently, all nodes reachable from \(X\)) is the set of all resource files loaded if resource
Xis loaded.
This theorem is self-evident and is exactly how the code is implemented (it recursively loads the dependency, a DFS).
Then, if we use \(T_X\) to indicate the set of nodes reachable from \(X\), and we use \(I_X\) to indicate the round number where resource X appears in the license file, and \(S_X\) to indicate the counter[X] at the end of processing all licenses (the expected value), we have our second theorem
S_X = \sum_{Y \mid X \in T_Y} I_Y
$$
Literally, if a node \(Y\) can reach \(X\), then the sum of round number of all such resource Y will be the final result of the counter value for resource X. Note that node \(X\) can reach itself.
With this information, You could construct a system of 10000 linear equations with 10000 unknowns (!) and try to solve it under the integer ring. However, there’s a faster way if we do more thinking.
For our theorem 3, notice that \(S_X = I_X\) whenever \(\forall u \neq X, X \notin T_u\). That is, if there’s no node that can reach \(X\) (except for \(X\) itself), then the final counter value is equal to the round number for resource X. Hopefully the proof is self-evident from Theorem 2.
That means, we could found all such nodes and figure out their positions in the license file. However, despite knowing that, how do we get the rest? Here comes our fourth theorem:
- If a dependency graph is acyclic, then removing a node with zero indegree (node that have no incoming edges) would result in either an empty graph, or a directed acyclic graph with at least one node with zero indegree.
This theorem is in fact a key property underlying Kahn’s algorithm for topological sorting, which only works for a directed acyclic graph. The proof of which would not be explained here.
Finally, for our theorem 5, we argue that if we remove a node \(X\) with zero indegree, and we subtract its round number from all nodes reachable from \(X\), then we have a new graph that satisfies all theorems above, or an empty graph. Mathematically speaking, it is
\forall u\text{ where indeg}(u) = 0, \forall X \text{ where } X \in T_u\\ S'_X = S_X – I_u = \sum_{Y\neq u \mid X\in T_Y} I_Y
$$
Where \(S’\) is the counter value for the new graph. The proof hopefully should also be self-evident.
With everything above, we have our algorithm to find the order of resource IDs expected in the license file, which follows the same structure as Kahn’s algorithm:
counters := [<expected final counter values>]
rounds := [None] * 10000
while graph is not empty:
u := node with zero indegree # must exist (theorem 4)
rounds[u] = counters[u] # theorem 3
for all v reachable from u:
counters[v] -= counters[u] # theorem 5
remove u from graph
This, in fact, is effectively the same as gaussian elimination, which is what is used if you were to construct a reachability matrix and solve the linear equations. Everything is connected…
There are some optimizations we could do, for example:
- Keep track of nodes without incoming edges so finding one takes constant time. To do that, we can construct a transpose graph (where all edge directions are reversed).
- Instead of decreasing counters for all nodes reachable from it, we use lazy update to accumulate values on the direct outgoing neighbors, and only update further when the node is being removed.
Taken together, the Python code would look something like this:
counters = []
with open('10000.exe', 'rb') as f:
f.seek(0xcae00)
for i in range(10000):
counters.append(int.from_bytes(f.read(4), 'little'))
transpose_graph = defaultdict(list)
for k, vs in graph.items():
for v in vs:
transpose_graph[v].append(k)
rounds = [None] * 10000
lazy = [set() for _ in range(10000)]
zero_indegrees = [i for i in range(10000) if not transpose_graph.get(i)]
while zero_indegrees:
cur = zero_indegrees.pop()
round = counters[cur] - sum(lazy[cur])
rounds[cur] = round
lazy[cur].add(round)
for n in graph.get(cur, ()):
lazy[n] |= lazy[cur]
transpose_graph[n].remove(cur)
if not transpose_graph[n]:
zero_indegrees.append(n)
To get the order as they appear in the license, we just need a reverse mapping of rounds:
licenses = [None] * 10000
for i, r in enumerate(rounds):
assert licenses[r] is None
licenses[r] = i
Crypto (again?)
After recovering the expected resource ID order in the license file, we can use it to calculate the expected input buffer to DllMain for each round. I then used angr to try to solve it, but turns out it still couldn’t solve for the initial buffer. Apparently there are some techniques used to counter for symbolic execution.
After some more manual analysis, we first realized that there seem to have only three general shapes of those f functions:
For 1, it is clearly a substitution box where data[i] is substituted with mapping[data[i]]. By the way, this kind of non-linear substitution almost always defeats symbolic execution. Reversing this manually would be simple though, as we just need to construct a reverse mapping.
For 2, it is slightly more confusing, but should be quite obvious that it is a shuffle method. The local_38 stores a destination index for each of the 32 locations. The first for loop shuffles them to a local stack buffer, and the second for loop copies them back to the original buffer.
For 3, it is way more complicated. Time to ask AI:

It seems that the function is implementing a uint256 modular exponentiation. Furthermore, it saves and forces least significant bit to be set before doing the exponentiation, and restores it in the result. This is a common practice when dealing with the elliptic curve point that are encoded in a specific format (as explained by AI), but in this case it’s practically just adding obfuscation.
To reverse this, we need to essentially do a discrete log. It’s CRYPTO time! Fortunately, AI knows how to solve it (again):

After around 100 function calls consisting of these three types of functions, we are met with a large chunk of totally different logic.
v641 = 0xDC37C0E304978087LL;
v640 = 0x594B7F91F11228E5LL;
v618 = 0x264F1C2A310E43AALL;
v619 = 0;
v620 = 0x6F62577DDB8F7C8LL;
v621 = 0;
v622 = 0x2F5EEF5C62186C64LL;
v623 = 0;
v624 = 0x3B278B1EA0E08E88LL;
v625 = 0;
v626 = 0x30B6B0678E48AEEuLL;
v627 = 0x5857A70651B71BD1uLL;
v628 = 0x11328681BBF8806AuLL;
v629 = 0x46A52DF6F08B2685uLL;
v630 = 0x5B5746A4910CA7FDuLL;
v631 = 0x4FCE2F265662E21uLL;
v632 = 0x32A013DC0E0F538AuLL;
v633 = 0xFFFEC7AE2C6F8F79LL;
v634 = 0x3B0AD6E24BE21F00uLL;
v635 = 0xD285721394B26B6FLL;
v636 = 0x49FF24112A0C1A2EuLL;
v637 = 0xF3A55FBBC4837E78LL;
for ( i = 0; i <= 15; ++i )
{
v455 = &v616[2 * i + 120];
v456 = v455[1];
*v455 ^= *(_QWORD *)&a4[2 * (i % 4)];
v455[1] = v456;
if ( *(_OWORD *)&v616[2 * i + 120] >= v641 )
return 0;
}
v639 = 0u;
v458 = v618;
v459 = v619;
v460 = v627;
v607 = v637 * v632;
v606 = v641;
v461 = (__m128)sub_22417F250(v4, *((__int64 *)&v627 + 1), v627, (unsigned __int64 *)&v606, (unsigned __int64 *)&v607);
v607 = *(_OWORD *)&v461 * v460;
v606 = v641;
v601 = sub_22417F250(v461, *((__int64 *)&v460 + 1), v460, (unsigned __int64 *)&v606, (unsigned __int64 *)&v607);
v462 = v628;
v607 = v635 * v633;
v606 = v641;
v463 = (__m128)sub_22417F250(
(__m128)v601,
*((__int64 *)&v628 + 1),
v628,
(unsigned __int64 *)&v606,
(unsigned __int64 *)&v607);
v607 = *(_OWORD *)&v463 * v462;
v606 = v641;
v596 = sub_22417F250(v463, *((__int64 *)&v462 + 1), v462, (unsigned __int64 *)&v606, (unsigned __int64 *)&v607);
v464 = v629;
v607 = v636 * v631;
v606 = v641;
v465 = (__m128)sub_22417F250(
(__m128)v596,
*((__int64 *)&v629 + 1),
v629,
(unsigned __int64 *)&v606,
(unsigned __int64 *)&v607);
[...]
Time to ask AI again:

It didn’t do a good job for the middle part, because I forgot to give it context of what function sub_22417f250 does. Once I told it that it is a function that takes in two uint256 pointers and does arg1 % arg2 (which I also didn’t reverse and just asked AI), it could figure out the middle part easily:

The result of this calculation (the determinant) is compared with 0, and the code would return early if the determinant is 0. This is clearly to validate that the matrix is invertible.
Summarizing what we know now, the part after the f function calls contains 4 small parts:
- The input 32 bytes (after transformed by the
ffunction calls) is read in as 4uint64s and XOR’d with values on the stack (v616). Note that 16 values are produced, so that the 4uint64s are repeated 4 times. During this, a check is also done to make sure the values do not exceed the modulus (v641). - The determinant of the resulting matrix is calculated to make sure it is invertible.
- The matrix modular exponentiation is performed where the exponent is
v640and modulus atv641. - Final verification of
memcmpto make sure the result is expected, and returns true if it is.
We can ignore part 2 as it is only for validation. Part 1 is just XOR so we know how to reverse that as well.
However, to reverse part 3, we have to do a discrete log with matrix. If we were still in the era of no AI, I would definitely struggle to solve this, but fortunately AI comes to the rescue again:

And it gives the following code:
def recover_matrix(B, a, m):
"""
Recover A from B = A^a mod m
B: 4x4 matrix (A^a mod m)
a: known exponent
m: prime modulus
"""
# 1. Compute the group order (or exponent)
# For GL(4, F_m):
group_order = (m**4 - 1) * (m**4 - m) * (m**4 - m**2) * (m**4 - m**3)
# 2. Find modular inverse: k such that a*k ≡ 1 (mod group_order)
k = mod_inverse(a, group_order)
# 3. Compute A = B^k mod m
A = matrix_power(B, k, m)
return A
which works like a charm (while I have no idea why it works).
Parse and done
After analyzing seemingly everything, the rest is to hope that there are no sudden exceptions and everything we’ve seen are indeed everything there is.
To parse the constants on the stack, you could do regular expression on the disassembly or the decompiled code. If you know any scripting, it would probably work directly with Ghidra and IDA Pro as well. For me, similar to 7 and 8, I used Capstone to disassemble the instructions and parsed them on a syntax level.
I’ll summarize what I did here:
- For the main body of the
checkfunction, I wrote a state machine that transitions between different parts as analyzed above. Luckily, the instructions are mostly stable, so I could skip them by simply fast-forward certain bytes. - During the state that handles
ffunction parts, I have a helper function that identifies which one of the three types offfunction we are trying to parse, and then give it to the specific parser that actually does the parsing. - These 3 different parsers expose the same
backwardAPI that allows me to pass the output buffer in and return the expected input buffer. - The part after
ffunctions have mostly only to do with the stack values (constants for exponents and modulars) as the calculation is exactly the same. - There is also a global
Counterclass to emulate the counter array analyzed above.
There are three hiccups I encountered:
- The third
ffunction type (modular exponentiation) have the exponent only 120 bits, because somehow although there are 4movabsfor 64 bit immediate, the third immediate value is moved to a location 1 byte overlapping the second one. - For
ffunctions, they all begin with initially XORing with the counter array + some offset. For most of the programs the instruction isADD, but for a few they areSUB(why?). - Also, for the first resource, the offset is 0, so there are no
ADD/SUBinstructions.
Luckily, the script was still pretty efficient so I didn’t waste too much time.
My final script is as follows:
import json
import os
import cle
import capstone
from cst import *
from Crypto.Util.number import isPrime
import numpy as np
Cs = capstone.Cs(capstone.CS_ARCH_X86, capstone.CS_MODE_64)
Cs.detail = True
def extract_imm(insn, reg):
assert insn.mnemonic == 'movabs', insn
assert insn.operands[0].type == capstone.x86.X86_OP_REG, insn
assert insn.operands[0].reg == reg, insn
assert insn.operands[1].type == capstone.x86.X86_OP_IMM, insn
return insn.operands[1].imm
def counter_forward(counter: 'Counter', val: bytes):
assert len(val) == 32
assert 0 <= counter < 2**32
val = bytearray(val)
v = int.from_bytes(val[:4], 'little')
v ^= counter
val[:4] = v.to_bytes(4, 'little')
return bytes(val)
def counter_backward(counter: 'Counter', val: bytes):
assert len(val) == 32
assert 0 <= counter < 2**32
val = bytearray(val)
v = int.from_bytes(val[:4], 'little')
v ^= counter
val[:4] = v.to_bytes(4, 'little')
return bytes(val)
class SquAndMul:
def __init__(self, dll, addr, idx):
self.idx = idx
assert dll.read_mem(addr, len(SKIP_3)) == SKIP_3
addr += len(SKIP_3)
insns = list(Cs.disasm(dll.read_mem(addr, 16 * 6), addr, count=6))
imm0 = extract_imm(insns[0], capstone.x86.X86_REG_RAX) & ((1 << 64) - 1)
imm1 = extract_imm(insns[1], capstone.x86.X86_REG_RDX) & ((1 << 64) - 1)
assert insns[2].bytes == b'\x48\x89\x45\xa0'
assert insns[3].bytes == b'\x48\x89\x55\xa8'
imm2 = extract_imm(insns[4], capstone.x86.X86_REG_RAX) & ((1 << 64) - 1)
imm3 = extract_imm(insns[5], capstone.x86.X86_REG_RDX) & ((1 << 64) - 1)
addr += sum(i.size for i in insns)
assert dll.read_mem(addr, len(SKIP_4)) == SKIP_4
self.exp = imm0 | (imm1 << 64) | (imm2 << (128 - 8)) | (imm3 << (192 - 8))
self.rev_exp = pow(self.exp, -1, 2**255)
def forward(self, counter: 'Counter', val: bytes):
val = counter_forward(counter.get(self.idx), val)
v = int.from_bytes(val, 'little')
is_odd = v & 1
v |= 1
v = pow(v, self.exp, 2 ** (32 * 8))
res = bytearray(v.to_bytes(32, 'little'))
res[0] ^= is_odd ^ 1
return bytes(res)
def backward(self, counter: 'Counter', val: bytes):
assert len(val) == 32
val = bytearray(val)
is_odd = val[0] & 1
val[0] |= 1
v = int.from_bytes(val, 'little')
v = pow(v, self.rev_exp, 2 ** (32 * 8))
val = bytearray(v.to_bytes(32, 'little'))
val[0] ^= is_odd ^ 1
return counter_backward(counter.get(self.idx), val)
class SubTable:
def __init__(self, dll, addr, idx):
self.idx = idx
assert dll.read_mem(addr, len(SKIP_5)) == SKIP_5
addr += len(SKIP_5)
self.sbox = []
insns = list(Cs.disasm(dll.read_mem(addr, 16 * 16 * 4), addr, count=16 * 4))
for i in range(16):
imm0 = extract_imm(insns[i * 4 + 0], capstone.x86.X86_REG_RAX) & ((1 << 64) - 1)
imm1 = extract_imm(insns[i * 4 + 1], capstone.x86.X86_REG_RDX) & ((1 << 64) - 1)
self.sbox.extend(imm0.to_bytes(8, 'little'))
self.sbox.extend(imm1.to_bytes(8, 'little'))
addr += sum(i.size for i in insns)
assert dll.read_mem(addr, len(SKIP_6)) == SKIP_6
self.rbox = [None] * 256
for i, v in enumerate(self.sbox):
assert self.rbox[v] is None
self.rbox[v] = i
def forward(self, counter, val: bytes):
val = counter_forward(counter.get(self.idx), val)
return bytes(self.sbox[b] for b in val)
def backward(self, counter, val: bytes):
return counter_backward(counter.get(self.idx), tuple(self.rbox[b] for b in val))
class LocShuffle:
def __init__(self, dll, addr, idx):
self.idx = idx
assert dll.read_mem(addr, len(SKIP_7)) == SKIP_7
addr += len(SKIP_7)
self.locs = []
insns = list(Cs.disasm(dll.read_mem(addr, 16 * 2 * 4), addr, count=2 * 4))
for i in range(2):
imm0 = extract_imm(insns[i * 4 + 0], capstone.x86.X86_REG_RAX) & ((1 << 64) - 1)
imm1 = extract_imm(insns[i * 4 + 1], capstone.x86.X86_REG_RDX) & ((1 << 64) - 1)
self.locs.extend(imm0.to_bytes(8, 'little'))
self.locs.extend(imm1.to_bytes(8, 'little'))
self.rev_locs = [None] * 32
for i, v in enumerate(self.locs):
assert self.rev_locs[v] is None
self.rev_locs[v] = i
def forward(self, counter, val: bytes):
val = counter_forward(counter.get(self.idx), val)
new_val = bytearray(32)
for i, loc in enumerate(self.locs):
new_val[i] = val[loc]
return bytes(new_val)
def backward(self, counter, val: bytes):
new_val = bytearray(32)
for i, loc in enumerate(self.locs):
new_val[loc] = val[i]
return counter_backward(counter.get(self.idx), bytes(new_val))
class MatrixPow:
@staticmethod
def matrix_pow(mat, exp, modulo):
assert exp >= 0
assert mat.shape[0] == mat.shape[1]
res = np.eye(mat.shape[0], dtype=object)
base = mat.copy()
while exp > 0:
if exp & 1:
res = (res @ base) % modulo
base = (base @ base) % modulo
exp >>= 1
return res
def __init__(self, stack_vals):
_1344 = stack_vals[1344] & ((1 << 64) - 1)
_1352 = stack_vals[1352] & ((1 << 64) - 1)
self.modulo = _1344 | (_1352 << 64)
assert isPrime(self.modulo)
self.exp = stack_vals[1336] & ((1 << 64) - 1)
nums = []
for i in range(16, 264 + 1, 8):
nums.append(stack_vals[i] & ((1 << 64) - 1))
final = []
for i in range(16):
final.append(nums[i * 2] | (nums[i * 2 + 1] << 64))
final = np.array(final, dtype=object).reshape((4, 4))
nums = []
for i in range(1040, 1288 + 1, 8):
nums.append(stack_vals[i] & ((1 << 64) - 1))
xors = []
for i in range(16):
xors.append(nums[i * 2] | (nums[i * 2 + 1] << 64))
# phi = GL(4, F_m)
phi = (self.modulo ** 4 - 1) * (self.modulo ** 4 - self.modulo) * (self.modulo ** 4 - self.modulo ** 2) * (self.modulo ** 4 - self.modulo ** 3)
k = pow(self.exp, -1, phi)
ori = self.matrix_pow(final, k, self.modulo).reshape(16)
for i in range(16):
ori[i] ^= xors[i]
ori = ori.reshape((4, 4))
assert np.array_equal(ori[0], ori[1]) and np.array_equal(ori[0], ori[2]) and np.array_equal(ori[0], ori[3])
self.ori = bytearray()
for i in range(4):
self.ori.extend(ori[0][i].to_bytes(8, 'little'))
self.ori = bytes(self.ori)
class DLL:
loaded_dlls = dict()
@classmethod
def get(cls, idx):
if idx not in cls.loaded_dlls:
print(f'Loading DLL {idx:04d}')
cls.loaded_dlls[idx] = DLL(idx)
return cls.loaded_dlls[idx]
def __init__(self, idx):
self.idx = idx
self.counter_addr = None
self.loader = cle.Loader(f'dlls/{idx:04d}.dll', auto_load_libs=False)
self.parts = []
self.parsed_funcs = dict()
self.matpow = None
try:
self.__parse()
except RuntimeError as e:
raise Exception(f"Error parsing DLL {idx:04d}: {e}")
def __parse_func(self, addr):
original_addr = addr
if addr in self.parsed_funcs:
return self.parsed_funcs[addr]
sig = self.read_mem(addr, min(len(SIG_1), len(SIG_2), len(SIG_3)))
if SIG_1.startswith(sig):
addr += len(SIG_1)
elif SIG_2.startswith(sig):
addr += len(SIG_2)
elif SIG_3.startswith(sig):
addr += len(SIG_3)
else:
raise RuntimeError(f'Unknown function signature at {hex(addr)}')
insn1, insn2 = Cs.disasm(self.read_mem(addr, 16 * 2), addr, count=2)
# insn1: mov rax, [rip + <some_imm>]
assert insn1.mnemonic == 'mov', insn1
assert insn1.operands[0].type == capstone.x86.X86_OP_REG, insn1
assert insn1.operands[0].reg == capstone.x86.X86_REG_RAX, insn1
assert insn1.operands[1].type == capstone.x86.X86_OP_MEM, insn1
assert insn1.operands[1].mem.index == 0, insn1
assert insn1.operands[1].mem.scale == 1, insn1
assert insn1.operands[1].mem.base == capstone.x86.X86_REG_RIP, insn1
ct_addr = insn1.address + insn1.size + insn1.operands[1].mem.disp
if self.counter_addr is None:
self.counter_addr = ct_addr
assert self.counter_addr == ct_addr, insn1
if self.idx == 0:
addr += insn1.size
else:
# insn2: add rax, <some_imm>
if insn2.mnemonic == 'sub':
assert insn2.operands[0].type == capstone.x86.X86_OP_REG, insn2
assert insn2.operands[0].reg == capstone.x86.X86_REG_RAX, insn2
assert insn2.operands[1].type == capstone.x86.X86_OP_IMM, insn2
assert -insn2.operands[1].imm == self.idx * 4, insn2
else:
assert insn2.mnemonic == 'add', insn2
assert insn2.operands[0].type == capstone.x86.X86_OP_REG, insn2
assert insn2.operands[0].reg == capstone.x86.X86_REG_RAX, insn2
assert insn2.operands[1].type == capstone.x86.X86_OP_IMM, insn2
assert insn2.operands[1].imm == self.idx * 4, insn2
addr += insn1.size + insn2.size
if SIG_1.startswith(sig):
parsed = SquAndMul(self, addr, self.idx)
elif SIG_2.startswith(sig):
parsed = SubTable(self, addr, self.idx)
elif SIG_3.startswith(sig):
parsed = LocShuffle(self, addr, self.idx)
else:
raise RuntimeError(f'Unknown function type at {hex(addr)}')
self.parsed_funcs[original_addr] = parsed
return parsed
def __parse_func_name(self, name):
sym = self.loader.find_symbol(name)
return self.__parse_func(sym.rebased_addr)
def read_mem(self, addr, size):
return self.loader.memory.load(addr, size)
def __parse(self):
check_sym = self.loader.find_symbol('_Z5checkPh')
backers = list(self.loader.memory.backers(check_sym.rebased_addr))
code = None
for start, data in backers:
if start > check_sym.rebased_addr:
continue
if start - check_sym.rebased_addr > len(data):
continue
assert code is None
code = data[check_sym.rebased_addr - start:]
assert code is not None
state = 'prologue'
arg_off = None
extern_addr = None
rax_val = None
rdx_val = None
stack_vals = {}
skip_bytes = None
fixed_func = None
for insn in Cs.disasm(code, check_sym.rebased_addr):
if state == 'prologue':
if insn.mnemonic == 'push' and insn.operands[0].type == capstone.x86.X86_OP_REG:
continue
if insn.mnemonic == 'sub' and insn.operands[0].type == capstone.x86.X86_OP_REG and insn.operands[0].reg == capstone.x86.X86_REG_RSP and insn.operands[1].type == capstone.x86.X86_OP_IMM:
continue
if insn.mnemonic == 'lea' and insn.operands[0].type == capstone.x86.X86_OP_REG and insn.operands[0].reg == capstone.x86.X86_REG_RBP and insn.operands[1].type == capstone.x86.X86_OP_MEM and insn.operands[1].mem.base == capstone.x86.X86_REG_RSP:
continue
if insn.mnemonic == 'mov' and insn.operands[0].type == capstone.x86.X86_OP_MEM and insn.operands[0].mem.base == capstone.x86.X86_REG_RBP and insn.operands[1].type == capstone.x86.X86_OP_REG and insn.operands[1].reg == capstone.x86.X86_REG_RCX:
state = 'part1'
arg_off = insn.operands[0].mem.disp
continue
raise RuntimeError(f'unexpected instruction in prologue: {insn}')
if state == 'part1':
if insn.mnemonic != 'movabs':
# expect mov rax, [rbp + arg_off]
assert insn.mnemonic == 'mov', insn
assert insn.operands[0].type == capstone.x86.X86_OP_REG, insn
assert insn.operands[0].reg == capstone.x86.X86_REG_RAX, insn
assert insn.operands[1].type == capstone.x86.X86_OP_MEM, insn
assert insn.operands[1].mem.base == capstone.x86.X86_REG_RBP, insn
assert insn.operands[1].mem.disp == arg_off, insn
state = 'part1-2'
continue
else:
state = 'part2'
if state == 'part1-2':
# expect mov rcx, rax
assert insn.mnemonic == 'mov', insn
assert insn.operands[0].type == capstone.x86.X86_OP_REG
assert insn.operands[0].reg == capstone.x86.X86_REG_RCX, insn
assert insn.operands[1].type == capstone.x86.X86_OP_REG
assert insn.operands[1].reg == capstone.x86.X86_REG_RAX, insn
state = 'part1-3'
continue
if state == 'part1-3':
if insn.mnemonic == 'mov':
# expect mov rax, [rip + <some_addr>]
assert insn.operands[0].type == capstone.x86.X86_OP_REG, insn
assert insn.operands[0].reg == capstone.x86.X86_REG_RAX, insn
assert insn.operands[1].type == capstone.x86.X86_OP_MEM, insn
assert insn.operands[1].mem.base == capstone.x86.X86_REG_RIP, insn
assert insn.operands[1].mem.index == 0, insn
assert insn.operands[1].mem.scale == 1, insn
extern_addr = insn.address + insn.size + insn.operands[1].mem.disp
state = 'part1-4'
continue
# expect call <some_dllmain>
assert insn.mnemonic == 'call', insn
assert insn.operands[0].type == capstone.x86.X86_OP_IMM, insn
parsed = self.__parse_func(insn.operands[0].imm)
self.parts.append(parsed)
state = 'part1'
continue
if state == 'part1-4':
# expect call rax
assert insn.mnemonic == 'call', insn
assert insn.operands[0].type == capstone.x86.X86_OP_REG, insn
assert insn.operands[0].reg == capstone.x86.X86_REG_RAX, insn
for name, ext_sym in self.loader.main_object.imports.items():
if ext_sym.rebased_addr == extern_addr:
assert ext_sym.resolvewith.endswith('.dll')
assert len(ext_sym.resolvewith) == 8
idx = int(ext_sym.resolvewith[:-4], 10)
dll = DLL.get(idx)
self.parts.append(dll.__parse_func_name(name))
break
else:
raise RuntimeError(f'extern symbol at {hex(extern_addr)} not found')
state = 'part1'
continue
if state == 'part3':
if insn.mnemonic == 'lea':
skip_bytes = SKIP_2
state = 'part3-epi'
if state in ('part2', 'part3'):
if insn.mnemonic == 'movabs':
# expect mov rax, imm
assert insn.operands[0].type == capstone.x86.X86_OP_REG, insn
assert insn.operands[0].reg == capstone.x86.X86_REG_RAX, insn
assert insn.operands[1].type == capstone.x86.X86_OP_IMM, insn
rax_val = insn.operands[1].imm
continue
if insn.mnemonic == 'mov':
if insn.operands[0].type == capstone.x86.X86_OP_REG:
# expect mov edx, 0
assert insn.operands[0].reg == capstone.x86.X86_REG_EDX, insn
assert insn.operands[1].type == capstone.x86.X86_OP_IMM, insn
assert insn.operands[1].imm == 0, insn
rdx_val = 0
continue
if insn.operands[1].type == capstone.x86.X86_OP_REG:
if insn.operands[1].reg == capstone.x86.X86_REG_RAX:
# expect mov [rbp + ...], rax
assert insn.operands[0].type == capstone.x86.X86_OP_MEM, insn
assert insn.operands[0].mem.base == capstone.x86.X86_REG_RBP, insn
assert insn.operands[0].mem.index == 0, insn
assert insn.operands[0].mem.scale == 1, insn
assert rax_val is not None
disp = insn.operands[0].mem.disp
assert disp not in stack_vals
stack_vals[disp] = rax_val
rax_val = None
continue
if insn.operands[1].reg == capstone.x86.X86_REG_RDX:
# expect mov [rbp + ...], rdx
assert insn.operands[0].type == capstone.x86.X86_OP_MEM, insn
assert insn.operands[0].mem.base == capstone.x86.X86_REG_RBP, insn
assert insn.operands[0].mem.index == 0, insn
assert insn.operands[0].mem.scale == 1, insn
assert rdx_val == 0, insn
disp = insn.operands[0].mem.disp
assert disp not in stack_vals
stack_vals[disp] = 0
rdx_val = None
continue
if insn.operands[0].type == capstone.x86.X86_OP_MEM:
# expect mov [rbp + ...], 0
assert insn.operands[0].mem.base == capstone.x86.X86_REG_RBP, insn
assert insn.operands[0].mem.index == 0, insn
assert insn.operands[0].mem.scale == 1, insn
assert insn.operands[1].type == capstone.x86.X86_OP_IMM, insn
assert insn.operands[1].imm == 0, insn
continue
if insn.mnemonic == 'jmp':
assert insn.operands[0].type == capstone.x86.X86_OP_IMM, insn
assert insn.operands[0].imm - insn.address == 0xdd, insn
state = 'part2-epi'
skip_bytes = SKIP_1
continue
if state in ('part2-epi', 'part3-epi'):
if insn.mnemonic == 'call':
assert insn.operands[0].type == capstone.x86.X86_OP_IMM, insn
if fixed_func is None:
fixed_func = insn.operands[0].imm
assert fixed_func == insn.operands[0].imm, insn
skip_bytes = skip_bytes[len(insn.bytes):]
continue
assert skip_bytes[:len(insn.bytes)] == insn.bytes, insn
skip_bytes = skip_bytes[len(insn.bytes):]
if len(skip_bytes) == 0:
if state == 'part3-epi':
self.matpow = MatrixPow(stack_vals)
break
state = 'part3'
fixed_func = None
skip_bytes = None
continue
raise RuntimeError(f'unexpected state {state} at {insn}')
class Counter:
def __init__(self):
self.counters = [0] * 10000
with open('graph.json') as f:
graph_se = json.load(f)
self.graph = {int(k): v for k, v in graph_se.items()}
def __visit(self, node, idx, visited):
if node in visited:
if not visited[node]:
raise RuntimeError('Cycle detected')
return
visited[node] = False
self.counters[node] += idx
for neighbor in self.graph.get(node, ()):
self.__visit(neighbor, idx, visited)
visited[node] = True
def add(self, node, idx):
self.__visit(node, idx, dict())
def get(self, node):
return self.counters[node]
def main():
# 8928
with open('rounds.txt') as f:
rounds = json.load(f)
if os.path.exists('backup'):
print('Resuming from backup')
with open('backup', 'rt') as f:
backup = f.readlines()
else:
backup = []
counter = Counter()
for idx, node in enumerate(rounds):
print(f'round {idx}, node {node}')
if len(backup) <= idx:
dll = DLL.get(node)
ori = dll.matpow.ori
for part in reversed(dll.parts):
ori = part.backward(counter, ori)
backup.append(ori.hex() + '\n')
with open('backup', 'wt') as f:
f.writelines(backup)
counter.add(node, idx)
if __name__ == '__main__':
main()
Thank you for reading. This is my fifth, and probably my last time doing Flare-On challenge.
Thanks for all the fish.